seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
We define a primitive Pythagorean triad to be a triple of positive integers (a,b,c) with greatest common divisor 1 such that:
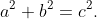
Examples of Pythagorean triads include (3,4,5) and (5,12,13).
In this question we find ALL primitive Pythagorean triads using high-school level methods.
Let Q denote the open first quadrant of the unit circle. (ie .)
.)
i) Prove that there is a one-to-one correspondence between the primitive Pythagorean triads and the points on Q with rational coordinates.
ii) Let denote the line through
denote the line through ) with gradient
with gradient  . Prove that
. Prove that  meets
meets 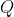 at a point with rational coordinates if and only if
at a point with rational coordinates if and only if 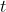 is rational.
is rational.
iii) Using the previous parts and the fact that a positive rational number can be written UNIQUELY in reduced form, find a parametric formula that gives every primitive Pythagorean triad.</t<1[></t<1[>
Examples of Pythagorean triads include (3,4,5) and (5,12,13).
In this question we find ALL primitive Pythagorean triads using high-school level methods.
Let Q denote the open first quadrant of the unit circle. (ie
i) Prove that there is a one-to-one correspondence between the primitive Pythagorean triads and the points on Q with rational coordinates.
ii) Let
iii) Using the previous parts and the fact that a positive rational number can be written UNIQUELY in reduced form, find a parametric formula that gives every primitive Pythagorean triad.</t<1[></t<1[>
Last edited:
