Since there are two possible values for a and c, we might need to consider a quadratic equation. Lets work backwards a little to see what quadratic we need.
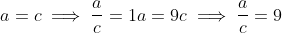
So this quadratic has roots of 1 and 9
\left(\frac{a}{c}-9\right)=\left(\frac{a}{c}\right)^2-10\left(\frac{a}{c}\right)+9)
We need to be on the lookout for something like this hopefully
now lets set up the equations
we'll let r be the common ratio between a,b,c

and for the arithmetic sequence we shall make the common difference be d
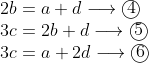
now what we have to do is to create an equation with only a and c (hopefully a quadratic), this can be done by finding two equations with just the variables a,b,c ie we need to find a way to remove r and d.
looking at equations
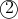
and
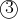
divide them to get
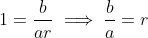
then we sub that new equation into
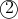
to take out the r...
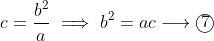
Now lets look at equations
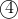
and
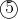
, subtract both of them to get
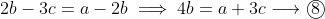
now that we have our two equations, lets sub
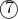
into
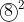
remove the b
^2\\16ac&=a^2+6ac+9c^2\\0&=a^2-10ac-9c^2\\0&=\left(\frac{a}{c}\right)^2-10\left(\frac{a}{c}\right)+9\ (\text{divide both sides by }c^2)\end{align})
yo it is da quad equation

, the rest should be pretty easy.