-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Square root x^2 = Absolute value x. Explain please (1 Viewer)
- Thread starter Alext_
- Start date
Kurosaki
True Fail Kid
Ok dude. The square root of something is always positive. So root x^2 will equal a positive number equal in magnitude to x.absolute of x- positive number equal in magnitude to x. The end 
Last edited:
Capt Rifle
Member
- Joined
- Jul 17, 2012
- Messages
- 399
- Gender
- Male
- HSC
- 2013
square root of x^2 is equal to plus or minusx, absolute value of x is always positive. so i dunno
Kurosaki
True Fail Kid
No the square root by itself is positive
Not sure if srssquare root of x^2 is equal to x, absolute value of x is always positive. So when you square root x^2 it will always be positive
Mate get ur facts rightNo the square root by itself is positive
Kurosaki
True Fail Kid
Wikipedia- the designation square root refers to the principal positive square rootMate get ur facts right
But yes if not using that designation I no what u mean lol. Not dat stupid
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,256
- Gender
- Male
- HSC
- 2012
When you say root 3, by convention you are assumed to mean the positive root. That's why in the quadratic formula say, its plus/minus the squareroot, because if you didn't have the plus/minus, you would only be taking the positive value.
Back to the original question, the squareroot of x^2 therefore must be the positive x solution, not -x, so its |x|
Back to the original question, the squareroot of x^2 therefore must be the positive x solution, not -x, so its |x|
DamTameNaken
Member
- Joined
- Sep 27, 2012
- Messages
- 48
- Gender
- Male
- HSC
- 2013
by convention the square root is always positive
x^2 = 16
in this case x can equal 4 or -4
sqrt(16)=x
x can only equal to 4
you always take the positive or principle root when you're square rooting. It's weird and it only works by convention but that's how it is.
x^2 = 16
in this case x can equal 4 or -4
sqrt(16)=x
x can only equal to 4
you always take the positive or principle root when you're square rooting. It's weird and it only works by convention but that's how it is.
Kurosaki
True Fail Kid
Lol oh well I got my mates to back me up  . lol Deswa start deleting old posts
. lol Deswa start deleting old posts 
Riproot
Addiction Psychiatrist
- Joined
- Nov 10, 2009
- Messages
- 8,228
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2017
it's not |x| it's x.When you say root 3, by convention you are assumed to mean the positive root. That's why in the quadratic formula say, its plus/minus the squareroot, because if you didn't have the plus/minus, you would only be taking the positive value.
Back to the original question, the squareroot of x^2 therefore must be the positive x solution, not -x, so its |x|
y = |x| is not always the same as y = x
is that right?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
The answer y=|x| is correct and this can be observed by considering y=root(f(x)), where f(x) =x^2, in a geometric sense.
Riproot
Addiction Psychiatrist
- Joined
- Nov 10, 2009
- Messages
- 8,228
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2017
The answer y=|x| is correct and this can be observed by considering y=root(f(x)), where f(x) =x^2, in a geometric sense.

Last edited:
OH1995
Member
- Joined
- Nov 7, 2011
- Messages
- 150
- Gender
- Male
- HSC
- 2013
+1 hahaThe answer y=|x| is correct and this can be observed by considering y=root(f(x)), where f(x) =x^2, in a geometric sense.
My maths teacher always drills into us that the square root of a perfect square is in fact the absolute value.
- Joined
- Feb 16, 2005
- Messages
- 8,390
- Gender
- Male
- HSC
- 2006
I'll try with an example.
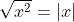
Let's consider for the example, the case that x = 2
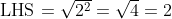

Hence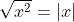 in this case
in this case
Now consider the case that x = -2
^2} = \sqrt{4} = 2)

Hence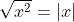 in this case
in this case
Now think about extensions to this for every single real number of x (if you can).
Let's consider for the example, the case that x = 2
Hence
Now consider the case that x = -2
Hence
Now think about extensions to this for every single real number of x (if you can).

