I will provide some information that will hopefully assist you in solving this question.
A sketch shows that AB > ɑ when its midpoint is closer to the centre than
^{\frac{1}{2}}=\frac{a\sqrt{3}}{2})
. The required probability is therefore
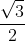
, matching the answer you provided.
Additionally, consider the following example of a similar question:
Two points A, B, are chosen on the circumference of a circle (see below) so that the angle at the centre is uniformly distributed over (0, π). What is the probability that the length of AB exceeds the radius of the circle?
Fix one end of the chord, then by elementary geometry, the chord exceeds the radius when the angle at the centre exceeds
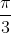
. Hence the required probability is:

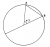
The length of the chord
)
, where ɑ is the radius of the circle and Φ the angle subtended at the centre by the chord.
=\text{Pr}\left(2a\:sin\:\frac{\phi }{2}\:\ge a\right))
)
But in the interval (0, π),
)
is an increasing function of Φ and
=\frac{1}{2})
, hence:
=\text{Pr}\left(\frac{\phi }{2}\ge \frac{\pi }{6}\right))
)
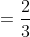
I hope this helps!
