Volume of solids of revolution
The area bounded by the parabola y =2x -x^2, the y-axis and the line y=1 is rotated about the x-axis. Find the volume generated.

So since it's asking about the revolution when that region is rotated about the x-axis, I set a=0 and b=1
and y^2= 4x^2-4x^3+x^4
so my formula ended up as V= pi [4x^3/3 - x^4 + x^5/5] b=1 on top and a=0 on bottom
= 8/15 pi
However, the answer in the textbook turned out to be different, giving something very confusing
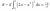
Anyone have a solution as to how they got that extra pi to minus the pi already in the formula?
The area bounded by the parabola y =2x -x^2, the y-axis and the line y=1 is rotated about the x-axis. Find the volume generated.

So since it's asking about the revolution when that region is rotated about the x-axis, I set a=0 and b=1
and y^2= 4x^2-4x^3+x^4
so my formula ended up as V= pi [4x^3/3 - x^4 + x^5/5] b=1 on top and a=0 on bottom
= 8/15 pi
However, the answer in the textbook turned out to be different, giving something very confusing
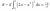
Anyone have a solution as to how they got that extra pi to minus the pi already in the formula?
