c) The fighter's position vector
r is given by
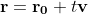
, where
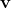
is the velocity vector and
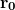
is the initial position of the fighter, and
t corresponds to the time elapsed (you could use
m instead of
t as the parameter, but
t seems more natural to me).
The velocity vector is found by dividing the displacement vector in my previous post by the time taken (which is
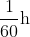
).
Hence
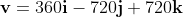
, where the units for the components of this vector are km/h. (Units of the scalar
t are hours, so
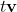
has units of km.)
So the fighter's position vector is
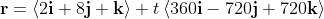
for

d) The position vector of the fighter is
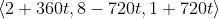
. Hence the squared distance of the fighter from the station (the origin) at any time is
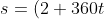^2 + (8-720t)^2 + (1+720t)^2)
.
To minimise distance, we can minimise squared distance.
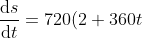-1440(8-720t)+1440(1+720t))
.
Set this to 0 to find minimum distance (if the solution is a positive
t, this corresponds to a positive time, hence a feasible solution).
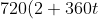-1440(8-720t)+1440(1+720t)=0 \Rightarrow t = \frac{1}{270})
.
Hence the fighter plane is closest when
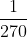
hours have passed.
Plugging in this value of
t to the fighter's position vector, we get the required point to be
)
.
e) required distance is
^2 + \left( \frac{16}{3}\right)^2 + \left( \frac{1}{3}\right)^2 }} \approx 6.30\mathrm{ km})
.
f) Done in my previous post. 1080 km/h
g) The fighter's rate of ascent or descent is given by the third component of the velocity vector, which is +720. Hence the plane is ascending at a rate of 720 km/h, or, in more natural units, 200 m/s.



