untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
i was trying to find the exact value of ) and i ended up with this equation with
and i ended up with this equation with 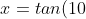) as a root
as a root
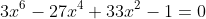
any ideas on how to go about solving it?
edit: dw i got it
 where
where 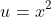
now use the cubic formula
abit tedious, anything else?
any ideas on how to go about solving it?
edit: dw i got it
now use the cubic formula
abit tedious, anything else?
Last edited:

