Ellipse (1 Viewer)

[hscishard]

Determine the real values of gamma for which the equation defines an ellipse (terry lee 5.1 q7)



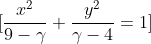
I got 4 < gamma < 6.5

Worked solution:
9-#>0
#<9
#-4>0
#>4
Therefore 4<#<9
The way the book did it doesn't seem right...

 

[Trebla]

The worked solution looks fine to me. How did you get the 6.5?

 

[hscishard]

I found an expression for the eccentricity and then went:
0 < e < 1

 

[iSplicer]

I found an expression for the eccentricity and then went:
0 < e < 1

Outline what you did =)

 

[hscishard]

gamma = z

z-4=(9-z)(1-e^2)

Found e to be [(2z-13)/(z-9)]^0.5

Then solved the inequality 0 < e < 1
Got the answer 4< z <6.5

 

[Trebla]

The flaw with that approach is that the relation assumes a > b (where (a,b) are the (x,y) intercepts). The ellipse still exists when a < b in which case

9 - γ = (γ - 4)(1 - e²)
=> 6.5 < γ < 9
if 0 < e < 1

Hence the full set of solutions are 4 < γ < 9

Note that γ = 6.5 is valid because e = 0 also leads to an ellipse (a circle is a special case of an ellipse)

The worked solution simply uses the fact that for an ellipse the 9 - γ and γ - 4 must be positive because they take the form a² and b² respectively.

b² = a²(1 - e²) only if a > b otherwise a² = b²(1 - e²)

 

[hscishard]

Oh ok thanks. Just found that part in cambridge 4u, unlike terry lee...

@Trebla what books did you use when you were taught maths; or did you get everything you needed from your teacher?