every time i do a past hsc paper i always lose marks in the transformations section ie when you're give y=f(x) and you sketch y=f(x^2), y=[f(x)]^2 etc etc...the only ones i can get out are the absolute value ones, all the others cost me marks  can anyone suggest a way to do those type of questions? it would REALLY be appreciated!
can anyone suggest a way to do those type of questions? it would REALLY be appreciated! 
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Graphs and transformations (1 Viewer)
- Thread starter miester
- Start date
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,419
- Gender
- Male
- HSC
- N/A
So using the function squared questions as an example... you have ^{2}) .
.
Let) therefore getting
therefore getting  . Now, the
. Now, the ) curve is the given curve (usually a diagram). The u axis is just the y axis.
curve is the given curve (usually a diagram). The u axis is just the y axis.
Draw the , and now we use this graph and the
, and now we use this graph and the ) to compare critical points, eg. x-intercept/s, y-intercept/s, asymptotes.
to compare critical points, eg. x-intercept/s, y-intercept/s, asymptotes.
So for example, when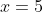 ,
,  , when
, when  ,
, 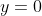 . Therefore we get
. Therefore we get )
...when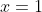 ,
,  , when
, when  ,
,  . Therefore we get
. Therefore we get )
...when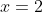 ,
, 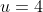 , when
, when 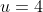 ,
,  . Therefore we get
. Therefore we get )
... and so on. Then the curve will usually take its shape.
It can work for sine, cosine, inverse, absolute values, exponentials, logs... you name it
Let
Draw the
So for example, when
...when
...when
... and so on. Then the curve will usually take its shape.
It can work for sine, cosine, inverse, absolute values, exponentials, logs... you name it
Last edited:
There is generally just a set of rules for 1/f(x). They are
f(x)=0 then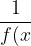}=\infty) (therefore when the original function crosses the x-axis it will become asymptote)
(therefore when the original function crosses the x-axis it will become asymptote)
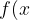}=\infty) then f(x)=0 (so it will cross the x-axis however this is not certain so when it reaches the x-axis we draw an open circle)
then f(x)=0 (so it will cross the x-axis however this is not certain so when it reaches the x-axis we draw an open circle)
if you draw the line y=1 then the same points at which the line intersects with the original graph, 1/f(x) will also pass through those points.
For the f(x^2) you can use the same method D94 has shown you.
So let u=x^2, now say you take the point A(2,4), x=2 therefore u=4. However the y value has not changed, the point A has just moved from (2,4) to (4,4).
Another example is point B(3,8), x=3 therefore u=9. The y value still remains unchanged, so the point B just moves from (3,8) to (9,8).
So the f(x) graph just becomes stretched when you do f(x^2).
f(x)=0 then
if you draw the line y=1 then the same points at which the line intersects with the original graph, 1/f(x) will also pass through those points.
For the f(x^2) you can use the same method D94 has shown you.
So let u=x^2, now say you take the point A(2,4), x=2 therefore u=4. However the y value has not changed, the point A has just moved from (2,4) to (4,4).
Another example is point B(3,8), x=3 therefore u=9. The y value still remains unchanged, so the point B just moves from (3,8) to (9,8).
So the f(x) graph just becomes stretched when you do f(x^2).
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,419
- Gender
- Male
- HSC
- N/A
Forwhat approach do you take when sketching 1/f(x) and f(x^2)?
With

