Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Second Question
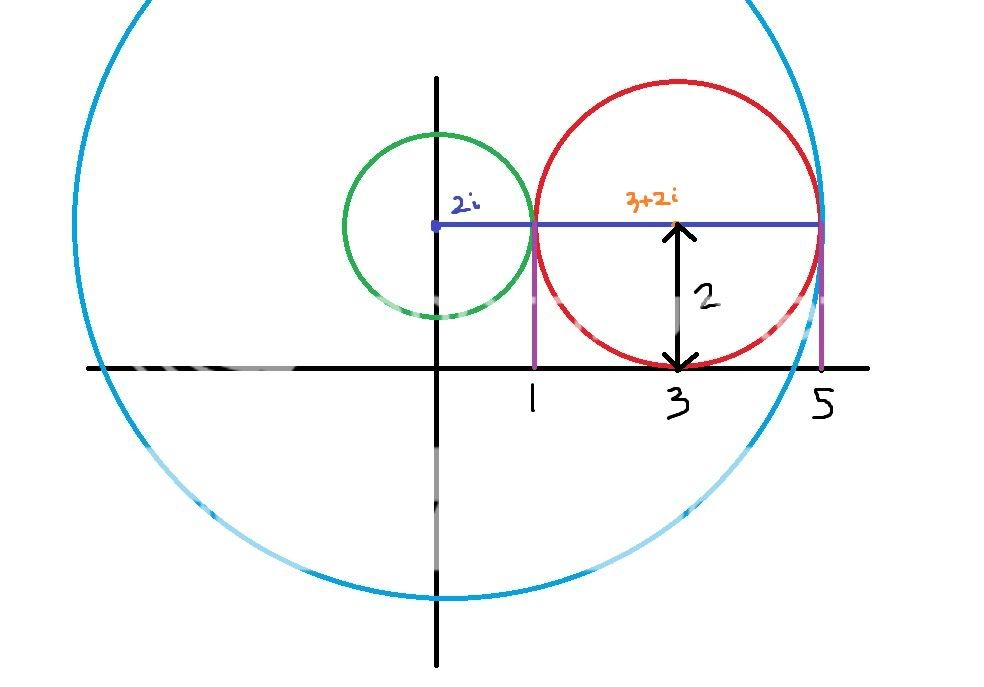
Observe the diagram. The two loci share the same y value for their centres. The green circle and the blue circle are the largest possible values of k for it to intersect with the red circle whilst having two solutions (well, strictly 1 solution, but we will be using an inequality).
Looking at the radius of the red circle (which is obviously 2 as defined by the locus), the green and blue circle can only intersect on either side of the red circle, in order to have 1 solution.
This occurs when x=1 and x=5.
However since the centre of the circle lies on the line x=0, we can safely say that these x co-ordinates will also be the radius of the blue/green circle.
But the radius of the blue/green circle is the value of k.
Hence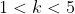
Second Question

Observe the diagram. The two loci share the same y value for their centres. The green circle and the blue circle are the largest possible values of k for it to intersect with the red circle whilst having two solutions (well, strictly 1 solution, but we will be using an inequality).
Looking at the radius of the red circle (which is obviously 2 as defined by the locus), the green and blue circle can only intersect on either side of the red circle, in order to have 1 solution.
This occurs when x=1 and x=5.
However since the centre of the circle lies on the line x=0, we can safely say that these x co-ordinates will also be the radius of the blue/green circle.
But the radius of the blue/green circle is the value of k.
Hence
Last edited:

