-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
2012 Year 9 &10 Mathematics Marathon (1 Viewer)
- Thread starter TerenceM
- Start date
Re: 2012 Year 9 &10 Mathematics Marathon
whats the point of posting up such difficult questions? everyone just searches the 'hardest question' they can find in hope to challenge someone with it. I mean comeon...we are doing 4unit math questions ffs TT.TT
whats the point of posting up such difficult questions? everyone just searches the 'hardest question' they can find in hope to challenge someone with it. I mean comeon...we are doing 4unit math questions ffs TT.TT
Re: 2012 Year 9 &10 Mathematics Marathon
And that simultaneous question, i remember that you need to use completing square method and that's pretty much it I think
lol that triangle question can be done just using pythagoras, ymcaec just did it the way that looked complicated by using the cosine rule.
And that simultaneous question, i remember that you need to use completing square method and that's pretty much it I think
Re: 2012 Year 9 &10 Mathematics Marathon
\\x^4+x^2y^2+y^4=741 ...(2) \end{matrix}\right\\\\$Rearrange $ (1)\\x^2+y^2=19+xy \\(x^2+y^2)^2=(19+xy)^2... (3)\\\\$Rearrange $(2)\\(x^2+y^2)^2=741+x^2y^2...(4)\\\\(3)=(4)\\(19+xy)^2=741+x^2y^2\\361+38xy+x^2y^2=741+x^2y^2\\38xy=380\\\therefore xy=10\\\therefore y=\frac{10}{x}\\\\$Substitute $y=\frac{10}{x}$ into $(1)\\x^2-10+\frac{100}{x^2}=19\\(x^2-25)(x^2-4)=0\\\therefore x=\pm 5$ or $\pm 2\\\\\therefore$ Solution: $(5,2), (-5,-2), (2,5), (-2,-5))
Here's another question. Solve for x and y:
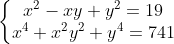
Last edited:
saysesame
Member
Re: 2012 Year 9 &10 Mathematics Marathon
Any more delicious maths questions?
Any more delicious maths questions?
Re: 2012 Year 9 &10 Mathematics Marathon
I'll check it moar carefully 2morrow
EDIT:Nvm correct
For your equation number 4, shouldn't it be 741-x^2y^2 instead?
I'll check it moar carefully 2morrow
EDIT:Nvm correct
Last edited:
zeebobDD
Member
- Joined
- Oct 23, 2011
- Messages
- 414
- Gender
- Male
- HSC
- 2012
Re: 2012 Year 9 &10 Mathematics Marathon
heres one for ya, show that the some of the numbers 1+2+3...+99+100 = 5050Any more delicious maths questions?
Re: 2012 Year 9 &10 Mathematics Marathon
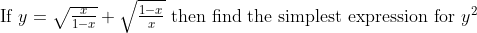
Re: 2012 Year 9 &10 Mathematics Marathon
^ymcaec, please wait a few hours until no one else can answer haha
^ymcaec, please wait a few hours until no one else can answer haha
zeebobDD
Member
- Joined
- Oct 23, 2011
- Messages
- 414
- Gender
- Male
- HSC
- 2012
Re: 2012 Year 9 &10 Mathematics Marathon
another question (procrastinating from school maths hw lol)
another question (procrastinating from school maths hw lol)
RealiseNothing
what is that?It is Cowpea
bluecrisps
Member
- Joined
- Jan 17, 2012
- Messages
- 106
- Gender
- Undisclosed
- HSC
- 2014
Re: 2012 Year 9 &10 Mathematics Marathon
Therefore y=36-2x (rearrange the equation)
ii) Area= length x height
= x x y
Sub Equation from B)i)
= x(36-2x)
= 36x x 2x^2
iii) Axis of symmetry= -b/2a
= -36/2(-2)
= -36/-4
= 9
This is the maximum value of x as it is the axis of symmetry for a parabola
iv) A=36x x 2x^2
= 36(9) -2(9)^2
= 329-162
= 167 cm2
b) i) 2x+y=36 (width of material)another question (procrastinating from school maths hw lol)
Therefore y=36-2x (rearrange the equation)
ii) Area= length x height
= x x y
Sub Equation from B)i)
= x(36-2x)
= 36x x 2x^2
iii) Axis of symmetry= -b/2a
= -36/2(-2)
= -36/-4
= 9
This is the maximum value of x as it is the axis of symmetry for a parabola
iv) A=36x x 2x^2
= 36(9) -2(9)^2
= 329-162
= 167 cm2
Re: 2012 Year 9 &10 Mathematics Marathon
It might seem very HSC-like with the maximum/minimum stuff, but it's really just a simple application of quadratics in year 10
however there's a calculation error in the last few steps,
$)
yes
It might seem very HSC-like with the maximum/minimum stuff, but it's really just a simple application of quadratics in year 10
Correct
however there's a calculation error in the last few steps,
Re: 2012 Year 9 &10 Mathematics Marathon
The q looks like part of a hsc paper to me...
Re: 2012 Year 9 &10 Mathematics Marathon
there's plenty more where that came from
(just PM me)
no, it's actually cut and pasted from a past year 10 yearly exam
there's plenty more where that came from
(just PM me)
Re: 2012 Year 9 &10 Mathematics Marathon
post up another question
Oh alrightyno, it's actually cut and pasted from a past year 10 yearly exam
there's plenty more where that came from
(just PM me)
post up another questionbluecrisps
Member
- Joined
- Jan 17, 2012
- Messages
- 106
- Gender
- Undisclosed
- HSC
- 2014
Re: 2012 Year 9 &10 Mathematics Marathon
Oops, darned windows calc -_-yes
It might seem very HSC-like with the maximum/minimum stuff, but it's really just a simple application of quadratics in year 10
Correct
however there's a calculation error in the last few steps,