HSC 2012-14 MX2 Integration Marathon (archive) (6 Viewers)

SpiralFlex · Aug 6, 2012

Re: MX2 Integration Marathon

$$Show that if$\; \int \frac{1}{uf(u)}\; du=F(u)+C, \;$then$\; \int \frac{m}{xf(x^m)}}\;dx = F(x^m)+C$

$Find:$

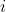$$i)$\; \int \frac{1}{x^n-x}\;dx$

$$ii)$\; \int \frac{1}{\sqrt{x^n+x^2}}\;dx$

SpiralFlex · Aug 6, 2012

Re: MX2 Integration Marathon

asianese said:
$\begin{align*}\int e^x\sin^2x\;dx&= \frac{1}{2}\int e^x(1-\cos2x)dx\\&= \frac{1}{2} \int (e^x-e^x\cos2x )dx\\ \text{Do integration by parts on}\; e^x\cos2x \; \text{with } u=\cos2x \; \text{and} \; dv=e^xdx \\ \therefore du=-2\sin2xdx \;\text{and}\; v=e^x \\ I&= \frac{1}{2} \left[ e^x-(\cos2xe^x+\int 2\sin2x e^x \; dx) \right ]\\ &= \frac{1}{2} \left[e^x-\cos2xe^x-2\int \sin2xe^x\;dx \right ]\\ &= \frac{e^x}{2}-\frac{\cos2xe^x}{2} -\int \sin2xe^x\;dx\\\text{Now use integration by parts on } \sin2xe^x \; \text{with } s=\sin2x \text{ and } dt=e^xdx \\ \therefore ds=2\cos2xdx \text{ and } t=e^x\\I&=\frac{e^x}{2}-\frac{\cos2xe^x}{2}-e^x\sin2x+2\int e^x(1-2\sin^2x)\\ &=\frac{e^x}{2}-\frac{\cos2xe^x}{2}-e^x\sin2x+2e^x-4I\\ 5I&=\frac{e^x}{2}-\frac{\cos2xe^x}{2}-e^x\sin2x+2e^x\\ \therefore I=\frac{e^x}{10}-\frac{\cos2xe^x}{10}-\frac{e^x\sin2x}{5}+\frac{2e^x}{5}+C \end{align*}$

Taburaaa integrasian.

asianese · Aug 6, 2012

Re: MX2 Integration Marathon

??

U MAD BRO · Aug 6, 2012

Re: MX2 Integration Marathon

Sanjeet said:
Lol so simple, can't believe no one got it before

yeah, i knew it was a substitution

but didn't do the first step

seanieg89 · Aug 6, 2012

Re: MX2 Integration Marathon

Find a recursion relation for the following sequence of integrals:

$I_n=\int e^x \sin^n(x) \, dx$

where n is a non-negative integer.

Hence evaluate $I_5$ .

abecina · Aug 6, 2012

Re: MX2 Integration Marathon

$\int \frac{\sin^{-1} \sqrt{x} -\cos^{-1} \sqrt{x}}{\sin^{-1} \sqrt{x} +\cos^{-1} \sqrt{x}} dx$

abecina · Aug 6, 2012

Re: MX2 Integration Marathon

$\int_0^1 \frac{\log(x+1)}{1+x^2} dx$

asianese · Aug 6, 2012

Re: MX2 Integration Marathon

Are you sure the second integral works?

abecina · Aug 6, 2012

Re: MX2 Integration Marathon

yep

rolpsy · Aug 6, 2012

Re: MX2 Integration Marathon

abecina said:
$\int_0^1 \frac{\log(x+1)}{1+x^2} dx$

$I = \int^1_0 \frac{\ln(x+1)}{1+x^2} \, \mathrm{d}x\\\\\begin{align*}\textup{Let } x = \frac{1-u}{1+u} = \frac{2}{1+u} - 1 \textup{, so } \mathrm{d}x = -\frac{2}{(1+u)^2} \, \mathrm{d}u\end{align*}\\\begin{align*}I &= \int^0_1 \frac{\ln\left ( \frac{2}{1+u} \right )}{1 + \frac{(1-u)^2}{(1+u)^2}} \times -\frac{2}{(1+u)^2} \, \mathrm{d}u\\&= \int^1_0 \frac{2\left (\ln(2) - \ln(1+u) \right )}{1 + 2u + u^2 + 1 - 2u + u^2} \, \mathrm{d}u\\&= \int^1_0 \frac{\ln(2) - \ln(1+u) }{1 + u^2} \, \mathrm{d}u\\2I&= \int^1_0 \frac{\ln(2)}{1 + u^2} \, \mathrm{d}u\\&=\ln(2) \times \frac{\pi}{4}\end{align*}$

$I = \frac{\pi}{8}\ln(2)$

edit:

abecina said:
$\int \frac{\sin^{-1} \sqrt{x} -\cos^{-1} \sqrt{x}}{\sin^{-1} \sqrt{x} +\cos^{-1} \sqrt{x}} dx$

use the fact that:

$\sin^{-1}\left ( \theta \right ) + \cos^{-1} \left ( \theta \right ) = \frac{\pi}{2}$

so

$\begin{align*}I &=\int \frac{\sin^{-1} \left ( \sqrt{x} \right ) - \cos^{-1} \left ( \sqrt{x} \right )}{\sin^{-1} \left ( \sqrt{x} \right ) + \cos^{-1} \left ( \sqrt{x} \right )} \, \mathrm{d}x\\&=\frac{2}{\pi} \int 2\sin^{-1}\left (\sqrt{x} \right ) - \frac{\pi}{2} \, \mathrm{d}x\end{align*}$

then use substitution, parts, etc.
I can't be bothered.

Nooblet94 · Aug 8, 2012

Re: MX2 Integration Marathon

$\int_0^{\frac{\pi}{4}} \ln (1+\tan x)dx$

U MAD BRO · Aug 8, 2012

Re: MX2 Integration Marathon

Nooblet94 said:
$\int_0^{\frac{\pi}{4}} \ln (1+\tan x)dx$

$\int_{0}^{\frac{\pi }{4}}ln(1+tan(\frac{\pi }{4}-x))$

Now, note that:

$tan(\frac{\pi }{4}-x)=\frac{sin(\frac{\pi }{4}-x)}{cos(\frac{\pi }{4}-x)}=\frac{sin(\frac{\pi }{4})cos(x)-cos(\frac{\pi }{4})sin(x)}{cos(\frac{\pi }{4})cos(x)+sin(\frac{\pi }{4})sin(x)}=\frac{cos(x)-sin(x)}{cos(x)+sin(x)}=\frac{1-tan(x)}{1+tan(x)}$

therefore our integral can be written as $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+\frac{1-tan(x)}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln\left (\frac{2}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln(2)-ln(1+tan(x))$

therefore $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+tan(x))dx=\int_{0}^{\frac{\pi }{4}}\frac{ln(2)}{2}=\frac{\pi ln(2)}{8}$

EDIT: LOL FORGOT TO INTEGRATE.

U MAD BRO · Aug 8, 2012

Re: MX2 Integration Marathon

U MAD BRO said:
$\int_{0}^{\frac{\pi }{4}}ln(1+tan(\frac{\pi }{4}-x))$

Now, note that:

$tan(\frac{\pi }{4}-x)=\frac{sin(\frac{\pi }{4}-x)}{cos(\frac{\pi }{4}-x)}=\frac{sin(\frac{\pi }{4})cos(x)-cos(\frac{\pi }{4})sin(x)}{cos(\frac{\pi }{4})cos(x)+sin(\frac{\pi }{4})sin(x)}=\frac{cos(x)-sin(x)}{cos(x)+sin(x)}=\frac{1-tan(x)}{1+tan(x)}$

therefore our integral can be written as $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+\frac{1-tan(x)}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln\left (\frac{2}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln(2)-ln(1+tan(x))$

therefore $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+tan(x))dx=\int_{0}^{\frac{\pi }{4}}\frac{ln(2)}{2}=\frac{\pi }{4}ln(2)$

Fixed!

rolpsy · Aug 8, 2012

Re: MX2 Integration Marathon

U MAD BRO said:
my solution is mathematically correct, i don't care if it's wrong

lol you forgot to integrate!

$\int^{\frac{\pi}{4}}_{0} \ln(2) \, \mathrm{d}x = \frac{\pi}{4}\ln(2)$

which gives the correct answer

here is a really difficult one:

$\int^{\frac{\pi}{2}}_{0} \frac{x}{\tan(x)} \, \mathrm{d}x$

good luck

asianese · Aug 8, 2012

Re: MX2 Integration Marathon

that x/tanx is my mission for tonight...have currently tried trig subs, t subs, nothing...have tried int fx from 0 to a = f(a-x) 0 to a...hasn't worked.

Shadowless · Aug 8, 2012

Re: MX2 Integration Marathon

U MAD BRO said:

$\int_{0}^{\frac{\pi }{4}}ln(1+tan(\frac{\pi }{4}-x))$

Click to expand...

U MAD BRO said:
Now, note that:

$tan(\frac{\pi }{4}-x)=\frac{sin(\frac{\pi }{4}-x)}{cos(\frac{\pi }{4}-x)}=\frac{sin(\frac{\pi }{4})cos(x)-cos(\frac{\pi }{4})sin(x)}{cos(\frac{\pi }{4})cos(x)+sin(\frac{\pi }{4})sin(x)}=\frac{cos(x)-sin(x)}{cos(x)+sin(x)}=\frac{1-tan(x)}{1+tan(x)}$

therefore our integral can be written as $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+\frac{1-tan(x)}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln\left (\frac{2}{1+tan(x)} \right )=\int_{0}^{\frac{\pi }{4}}ln(2)-ln(1+tan(x))$

therefore $\int_{0}^{\frac{\pi }{4}}ln\left ( 1+tan(x))dx=\frac{ln(2)}{2}$

i'm not particularly 'good' at 4u but correct me if i'm wrong in saying that:

tan x DOES NOT EQUAL tan( pi/4 - x )?

rather it equals tan ( pi/2 - x )

Shadowless · Aug 8, 2012

Re: MX2 Integration Marathon

rolpsy said:
lol you forgot to integrate!

$\int^{\frac{\pi}{4}}_{0} \ln(2) \, \mathrm{d}x = \frac{\pi}{4}\ln(2)$

which gives the correct answer

here is a really difficult one:

$\int^{\frac{\pi}{2}}_{0} \frac{x}{\tan(x)} \, \mathrm{d}x$

good luck

is the answer: pi/2 ?

(if the answer is right, i'll post solution when i figure out how to do all those integral signs and fractions = / )

rolpsy · Aug 8, 2012

Re: MX2 Integration Marathon

Shadowless said:
is the answer: pi/2 ?

(if the answer is right, i'll post solution when i figure out how to do all those integral signs and fractions = / )

sorry, nope
(although interested to know your method)

Shadowless said:
i'm not particularly 'good' at 4u but correct me if i'm wrong in saying that:

tan x DOES NOT EQUAL tan( pi/4 - x )?

rather it equals tan ( pi/2 - x )

s/he's using properties of definite integrals, namely

$\int^a_0 f(x) \, \mathrm{d}x = \int^a_0 f(a-x) \, \mathrm{d}x$

also tan(pi/2 - x) = cot(x)

nightweaver066 · Aug 8, 2012

Re: MX2 Integration Marathon

Shadowless said:
i'm not particularly 'good' at 4u but correct me if i'm wrong in saying that:

tan x DOES NOT EQUAL tan( pi/4 - x )?

rather it equals tan ( pi/2 - x )

Definite integral property.

$\int^a_0 f(x) dx = \int^a_0 f(a - x)dx$

If you wish to prove, let u = a - x for LHS and proceed.

nightweaver066 · Aug 8, 2012

Re: MX2 Integration Marathon

rolpsy said:
lol you forgot to integrate!

$\int^{\frac{\pi}{4}}_{0} \ln(2) \, \mathrm{d}x = \frac{\pi}{4}\ln(2)$

which gives the correct answer

here is a really difficult one:

$\int^{\frac{\pi}{2}}_{0} \frac{x}{\tan(x)} \, \mathrm{d}x$

good luck

$\int^{\frac{\pi}{2}}_0 \frac{x}{tanx}dx$

$= \int^{\frac{\pi}{2}}_0 xcotxdx$

$= [xln|sinx|]^{\frac{\pi}{2}}_0 - \int^{\frac{\pi}{2}}_0 ln|sinx|dx$

Now IIRC, that second integral is easily done by 2 applications of IBP and rearrangements.

D: i just realised its undefined at x = 0.. L'Hopital's rule?

HSC 2012-14 MX2 Integration Marathon (archive) (6 Viewers)

Well-Known Member

Well-Known Member

Σ

Member

Well-Known Member

Member

Member

Σ

Member

Member

Premium Member

Member

Member

Member

Σ

Member

Member

Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 6)