Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013-14 MX1 Marathon (archive) (1 Viewer)
- Thread starter SpiralFlex
- Start date
- Status
- Not open for further replies.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 3U Marathon Thread

This is just the sum of the row of Pascal's triangle, which is
row of Pascal's triangle, which is 
Considering Pascal's triangle, we know that the sum of two adjacent numbers is the number directly below them. Hence we can write the question as the sum of the numbers in the row above it:
This is just the sum of the
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Very elegant, nice work, my way was a little longer by considering expansions of (1+x)^2n and (1-x)^2nConsidering Pascal's triangle, we know that the sum of two adjacent numbers is the number directly below them. Hence we can write the question as the sum of the numbers in the row above it:
This is just the sum of therow of Pascal's triangle, which is

Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 3U Marathon Thread
Err, not true. The last term on the LHS alone is greater than the RHS...A nice result I've proven

Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
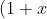^n + (1+x)^{n+1} + \dots + (1+x)^{2n} = \frac{(1+x)^n ((1+x)^n -1)}{(1+x)-1} = \frac{(1+x)^{2n}-(1+x)^n}{x} )
Equate co-efficient of x^n on both sides of equation. Anything illegal in the proof?
I considered the geometric series:Err, not true. The last term on the LHS alone is greater than the RHS...
Equate co-efficient of x^n on both sides of equation. Anything illegal in the proof?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
======================
New result:

(n+2)} )
:/ Can't believe I missed that, thanks for the heads up. I'll ask this question again once everyone has forgotten about it.Yes. Check the number of terms on the LHS, there are n+1, not n. A minor change needs to be made to your formula for the sum of a finite geometric series.
======================
New result:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
^n \ dx ) (which we can derive easily)
(which we can derive easily)
Use u-substitution, we yield the RHS.
Note that the LHS is::/ Can't believe I missed that, thanks for the heads up. I'll ask this question again once everyone has forgotten about it.
======================
New result:
(n+2)} )
Use u-substitution, we yield the RHS.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 3U Marathon Thread
^2 + (x+1)^2 - x^2 - (x-1)^2)


)
Now we will note that:
 + (x+1) + x + (x-1) = 4x+2)
So the sum of each group of four is just two times the sum of that group. Hence if we were to do it to all groups of four up to 100, we would get two times the sum of all the numbers from 1 to 100:
)
This is just double the 100th triangular number, which is just
So the answer is
Consider them in groups of four. Now consider the general case:
(The signs alternate in pairs)
(Provide proof of your value, either with latex or a brief outline of steps taken)
Now we will note that:
So the sum of each group of four is just two times the sum of that group. Hence if we were to do it to all groups of four up to 100, we would get two times the sum of all the numbers from 1 to 100:
This is just double the 100th triangular number, which is just
So the answer is
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Alternatively:

Difference of 2 squares
(100+98) + (99-97)(99+97) + \dots + (3-1)(3+1) )
Note that first bracket in each term is 2, take common:
 = \cdot 100 \cdot 101 = 10100 )
Elegant, nice workConsider them in groups of four. Now consider the general case:
Now we will note that:
So the sum of each group of four is just two times the sum of that group. Hence if we were to do it to all groups of four up to 100, we would get two times the sum of all the numbers from 1 to 100:
This is just double the 100th triangular number, which is just
So the answer is
Alternatively:
Difference of 2 squares
Note that first bracket in each term is 2, take common:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Capt Rifle
Member
- Joined
- Jul 17, 2012
- Messages
- 398
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
<a href="http://www.codecogs.com/eqnedit.php?latex=Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" target="_blank"><img src="http://latex.codecogs.com/gif.latex?Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" title="Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" /></a>
Edit: This is at a 3U difficulty, right guys?
<a href="http://www.codecogs.com/eqnedit.php?latex=Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" target="_blank"><img src="http://latex.codecogs.com/gif.latex?Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" title="Find \int cos^42x\, sin^32x\, \, dx\, \: using\, the\, subsitution\, u=cos2x" /></a>
Edit: This is at a 3U difficulty, right guys?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
I meant, prove your value :sI believe him.
- Status
- Not open for further replies.

