-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (4 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
100 HSC students are held captive in a room by an evil mathematician.
He writes down their names on 100 pieces of paper, and randomly puts them in 100 lined up boxes, one per box.
The prisoners get led to the box room one by one, and get a chance to check 50 boxes for their name, and then get sent to a third room, the boxes are closed again before the next prisoner comes in.
If each prisoner finds their own name successfully, then they all are released.
If even a single one fails, they are all killed.
i) What is the probability of survival if each chooses at random?
ii) (Not worth any marks) How high do you think we can make the probability of survival if the student's have some kind of strategy to their choices?
iii) What is the probability of survival if prisoner k opens box k first, then opens the box whose number is given by the piece of paper in box k, then continues opening boxes as directed by the number inside the previously opened box. If at some stage the instructed box is already open, he makes his next choice at random.
EDIT. If you are finding it too difficult to calculate iii), content yourself with finding a fairly simple and tight lower bound...this should be enough to surprise you.
100 HSC students are held captive in a room by an evil mathematician.
He writes down their names on 100 pieces of paper, and randomly puts them in 100 lined up boxes, one per box.
The prisoners get led to the box room one by one, and get a chance to check 50 boxes for their name, and then get sent to a third room, the boxes are closed again before the next prisoner comes in.
If each prisoner finds their own name successfully, then they all are released.
If even a single one fails, they are all killed.
i) What is the probability of survival if each chooses at random?
ii) (Not worth any marks) How high do you think we can make the probability of survival if the student's have some kind of strategy to their choices?
iii) What is the probability of survival if prisoner k opens box k first, then opens the box whose number is given by the piece of paper in box k, then continues opening boxes as directed by the number inside the previously opened box. If at some stage the instructed box is already open, he makes his next choice at random.
EDIT. If you are finding it too difficult to calculate iii), content yourself with finding a fairly simple and tight lower bound...this should be enough to surprise you.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Here is one to flex algebra muscles.
Consider the monic cubic equation z^3 + az^2 + bz + c = 0. (*)
Make a linear substitution of the form y = z + const. to obtain a cubic in y which has no quadratic term. Eg: y^3 = Ay + B.
Show that if 3st = A and s^3 + t^3 = B then y = s + t satisfies the previous equation.
Hence, using your knowledge of complex numbers, write down a expression for the three roots of (*) in terms of a,b,c. ie the cubic formulae.
Here is one to flex algebra muscles.
Consider the monic cubic equation z^3 + az^2 + bz + c = 0. (*)
Make a linear substitution of the form y = z + const. to obtain a cubic in y which has no quadratic term. Eg: y^3 = Ay + B.
Show that if 3st = A and s^3 + t^3 = B then y = s + t satisfies the previous equation.
Hence, using your knowledge of complex numbers, write down a expression for the three roots of (*) in terms of a,b,c. ie the cubic formulae.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
I think I just proved something pretty cool (yet elementary).
Let f be a function defined on the positive reals such that:
i) f is positive
ii) f is decreasing
iii) f is twice differentiable and f'' is always nonzero.
iv) any tangent to the graph of f makes a triangle of equal area with the x and y axes.
1. What can f be? (Hint: We perform these sorts of calculations all the time in conics, but in this questions our f is unknown. You will end up with an equation involving f and its derivative which must be satisfied. Use algebraic trickery to proceed from here. It might help if you can remember a function you have seen a lot that satisfies these properties.)
2. If we drop condition iii), do we get any more solutions?
I think I just proved something pretty cool (yet elementary).
Let f be a function defined on the positive reals such that:
i) f is positive
ii) f is decreasing
iii) f is twice differentiable and f'' is always nonzero.
iv) any tangent to the graph of f makes a triangle of equal area with the x and y axes.
1. What can f be? (Hint: We perform these sorts of calculations all the time in conics, but in this questions our f is unknown. You will end up with an equation involving f and its derivative which must be satisfied. Use algebraic trickery to proceed from here. It might help if you can remember a function you have seen a lot that satisfies these properties.)
2. If we drop condition iii), do we get any more solutions?
chris_power_96
Member
- Joined
- Aug 23, 2011
- Messages
- 111
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
Does anyone have any 2013 papers?
Does anyone have any 2013 papers?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Could you clarify what is meant by (iv), what does it mean to make a triangle of 'equal area' what is it equal to?I think I just proved something pretty cool (yet elementary).
Let f be a function defined on the positive reals such that:
i) f is positive
ii) f is decreasing
iii) f is twice differentiable and f'' is always nonzero.
iv) any tangent to the graph of f makes a triangle of equal area with the x and y axes.
1. What can f be? (Hint: We perform these sorts of calculations all the time in conics, but in this questions our f is unknown. You will end up with an equation involving f and its derivative which must be satisfied. Use algebraic trickery to proceed from here. It might help if you can remember a function you have seen a lot that satisfies these properties.)
2. If we drop condition iii), do we get any more solutions?
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
I think he means constant area?Could you clarify what is meant by (iv), what does it mean to make a triangle of 'equal area' what is it equal to?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Yep this. We don't care what this is equal to.I think he means constant area?
Last edited:
Makematics
Well-Known Member
Re: HSC 2013 4U Marathon

yes, i have a few for 4u. i will be passing them on to nerdasdasd soon, who will proceed to upload to his skydriveDoes anyone have any 2013 papers?
alexandred
New Member
- Joined
- Nov 8, 2011
- Messages
- 29
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
We had (f(x)-xf'(x))^2 * 1/f'(x) = const., differentiating we get f(x) = -xf'(x) and then ln(f(x)) = -lnx + C => f(x) = A/x for A>0
2. I couldn't see that I got any more solutions in this case, since I never ended up using the f" nonzero condition apart from cancelling it across an expression for the derivative of the above (never excluded a solution due to it).. I'm probably missing solutions here.
1. As the 'show area of triangle produced by tangent to hyperbola and asymptotes is constant,' but in this case just the rectangular hyperbola y = A/x.I think I just proved something pretty cool (yet elementary).
Let f be a function defined on the positive reals such that:
i) f is positive
ii) f is decreasing
iii) f is twice differentiable and f'' is always nonzero.
iv) any tangent to the graph of f makes a triangle of equal area with the x and y axes.
1. What can f be? (Hint: We perform these sorts of calculations all the time in conics, but in this questions our f is unknown. You will end up with an equation involving f and its derivative which must be satisfied. Use algebraic trickery to proceed from here. It might help if you can remember a function you have seen a lot that satisfies these properties.)
2. If we drop condition iii), do we get any more solutions?
We had (f(x)-xf'(x))^2 * 1/f'(x) = const., differentiating we get f(x) = -xf'(x) and then ln(f(x)) = -lnx + C => f(x) = A/x for A>0
2. I couldn't see that I got any more solutions in this case, since I never ended up using the f" nonzero condition apart from cancelling it across an expression for the derivative of the above (never excluded a solution due to it).. I'm probably missing solutions here.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Here is my attempt for (iii)
First, lets generalize this for (2n) unlucky HSC students.
Consider the sequences:
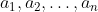
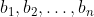
Now, instead of having the student 'k' picking a box, it will be student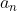
Now, the first sequence, simply describes a sequence of box pickings (based on that strategy) which will eventually yield a_n
So what this means is, the card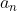 is in box
is in box 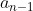 and card
and card 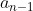 is in box
is in box 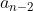
And so on, until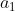
Whereas, the second sequence, is just every other option.
This means that if the student picks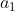 on his first go, he is will always eventually yield
on his first go, he is will always eventually yield 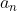 the desired result, just as if he picks
the desired result, just as if he picks 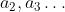 and so on.
and so on.
If on the students first go he picks one number from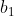
The student must rely on a repeat somewhere (which brings him to a box he has already uncovered), which allows him to have a chance at picking one box from the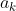 sequence.
sequence.
If the student picks boxes from the
boxes from the 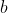 sequence, and encounters a repeat, he then has a chance to randomly pick a box from:
sequence, and encounters a repeat, he then has a chance to randomly pick a box from:
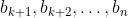
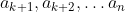
Since if he picks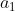 for instance, he will not be able to get to a_n in enough moves.
for instance, he will not be able to get to a_n in enough moves.
Therefore the probability that he picks a desired box is always 1/2 regardless of k, if he encounters a repeat.
These repeats can be seen as 'loops'
So if we loop:
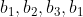
Then he gets a chance (1/2 chance) to get one of the 'a' boxes.
Indeed, a loop will always occur, unless the loop is 'n' long.
Therefore the probability that the student picks the right box is:
 \times \frac{1}{2^{k-1}} )
The 2^n is the amount of ways to split n things into any number of subsets, therefore the sum describes the probability of splitting n things into k groups and with those k groups, getting k repetitions and having none of them transfer on to the sequence
sequence
for example
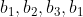
He randomly picks b_4 say (with 1/2 probability) and ends up in the seqeuence:
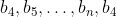
But by b_n, his amount of choices has ran out, ending the game
In this case, there are 2 'loops' from the n, and he has to deny entry into the 'a' sequence once.
Therefore 1/2^{k-1}, just as if there are 3 loops, he needs to deny entry into the 'a' sequence twice.

Since this does not differ student to student
^{2n} )
??
Well, I'm content with my logic, but as usual with probability, I find that I'm missing something somewhere.
100 HSC students are held captive in a room by an evil mathematician.
He writes down their names on 100 pieces of paper, and randomly puts them in 100 lined up boxes, one per box.
The prisoners get led to the box room one by one, and get a chance to check 50 boxes for their name, and then get sent to a third room, the boxes are closed again before the next prisoner comes in.
If each prisoner finds their own name successfully, then they all are released.
If even a single one fails, they are all killed.
i) What is the probability of survival if each chooses at random?
ii) (Not worth any marks) How high do you think we can make the probability of survival if the student's have some kind of strategy to their choices?
iii) What is the probability of survival if prisoner k opens box k first, then opens the box whose number is given by the piece of paper in box k, then continues opening boxes as directed by the number inside the previously opened box. If at some stage the instructed box is already open, he makes his next choice at random.
EDIT. If you are finding it too difficult to calculate iii), content yourself with finding a fairly simple and tight lower bound...this should be enough to surprise you.
Here is my attempt for (iii)
First, lets generalize this for (2n) unlucky HSC students.
Consider the sequences:
Now, instead of having the student 'k' picking a box, it will be student
Now, the first sequence, simply describes a sequence of box pickings (based on that strategy) which will eventually yield a_n
So what this means is, the card
And so on, until
Whereas, the second sequence, is just every other option.
This means that if the student picks
If on the students first go he picks one number from
The student must rely on a repeat somewhere (which brings him to a box he has already uncovered), which allows him to have a chance at picking one box from the
If the student picks
Since if he picks
Therefore the probability that he picks a desired box is always 1/2 regardless of k, if he encounters a repeat.
These repeats can be seen as 'loops'
So if we loop:
Then he gets a chance (1/2 chance) to get one of the 'a' boxes.
Indeed, a loop will always occur, unless the loop is 'n' long.
Therefore the probability that the student picks the right box is:
The 2^n is the amount of ways to split n things into any number of subsets, therefore the sum describes the probability of splitting n things into k groups and with those k groups, getting k repetitions and having none of them transfer on to the
for example
He randomly picks b_4 say (with 1/2 probability) and ends up in the seqeuence:
But by b_n, his amount of choices has ran out, ending the game
In this case, there are 2 'loops' from the n, and he has to deny entry into the 'a' sequence once.
Therefore 1/2^{k-1}, just as if there are 3 loops, he needs to deny entry into the 'a' sequence twice.
Since this does not differ student to student
??
Well, I'm content with my logic, but as usual with probability, I find that I'm missing something somewhere.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
There are actually non-hyperbolic solutions if we drop (iii), such as any line of the form ax+by=c (a,b,c > 0): the tangent at any point will be the line itself, so the constant area property is trivial. We could also patch together such linear solutions with hyperbolic solutions in a differentiable way to obtain funkier solutions.
Hey, nice. This is pretty much what I had in mind.1. As the 'show area of triangle produced by tangent to hyperbola and asymptotes is constant,' but in this case just the rectangular hyperbola y = A/x.
We had (f(x)-xf'(x))^2 * 1/f'(x) = const., differentiating we get f(x) = -xf'(x) and then ln(f(x)) = -lnx + C => f(x) = A/x for A>0
2. I couldn't see that I got any more solutions in this case, since I never ended up using the f" nonzero condition apart from cancelling it across an expression for the derivative of the above (never excluded a solution due to it).. I'm probably missing solutions here.
There are actually non-hyperbolic solutions if we drop (iii), such as any line of the form ax+by=c (a,b,c > 0): the tangent at any point will be the line itself, so the constant area property is trivial. We could also patch together such linear solutions with hyperbolic solutions in a differentiable way to obtain funkier solutions.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Good effort, from a skim read it seems some of the ideas are there. I will try to wrap my head around your notation a little more carefully later to see exactly what's going on, but something is going wrong because your expression is something like 0.99996 for n=50, which is well off what I am looking for.
Here is my attempt for (iii)
First, lets generalize this for (2n) unlucky HSC students.
Consider the sequences:
Now, instead of having the student 'k' picking a box, it will be student
Now, the first sequence, simply describes a sequence of box pickings (based on that strategy) which will eventually yield a_n
So what this means is, the cardis in box
and card
is in box
And so on, until
Whereas, the second sequence, is just every other option.
This means that if the student pickson his first go, he is will always eventually yield
the desired result, just as if he picks
and so on.
If on the students first go he picks one number from
The student must rely on a repeat somewhere (which brings him to a box he has already uncovered), which allows him to have a chance at picking one box from thesequence.
If the student picksboxes from the
sequence, and encounters a repeat, he then has a chance to randomly pick a box from:
Since if he picksfor instance, he will not be able to get to a_n in enough moves.
Therefore the probability that he picks a desired box is always 1/2 regardless of k, if he encounters a repeat.
These repeats can be seen as 'loops'
So if we loop:
Then he gets a chance (1/2 chance) to get one of the 'a' boxes.
Indeed, a loop will always occur, unless the loop is 'n' long.
Therefore the probability that the student picks the right box is:
The 2^n is the amount of ways to split n things into any number of subsets, therefore the sum describes the probability of splitting n things into k groups and with those k groups, getting k repetitions and having none of them transfer on to thesequence
for example
He randomly picks b_4 say (with 1/2 probability) and ends up in the seqeuence:
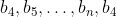
But by b_n, his amount of choices has ran out, ending the game
In this case, there are 2 'loops' from the n, and he has to deny entry into the 'a' sequence once.
Therefore 1/2^{k-1}, just as if there are 3 loops, he needs to deny entry into the 'a' sequence twice.
Since this does not differ student to student
??
Well, I'm content with my logic, but as usual with probability, I find that I'm missing something somewhere.
Good effort, from a skim read it seems some of the ideas are there. I will try to wrap my head around your notation a little more carefully later to see exactly what's going on, but something is going wrong because your expression is something like 0.99996 for n=50, which is well off what I am looking for.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
=====

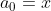
 \ \ \ $for$ \ \ k \geq 0 )

Ah well, can you post the solution soon if no one gets it?Good effort, from a skim read it seems some of the ideas are there. I will try to wrap my head around your notation a little more carefully later to see exactly what's going on, but something is going wrong because your expression is something like 0.99996 for n=50, which is well off what I am looking for.
=====
alexandred
New Member
- Joined
- Nov 8, 2011
- Messages
- 29
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Clearly f'(x) >= 0. When f'(x) = 0, we have x = 0 => f(x) = 0, or we have f(x) = 2npi - 0 > 0, and f(x) is increasing on all intervals between, easy to see that f(x) > 0
Then x > sin(x), since sin(x) AND x are odd we have |x| > |sinx| and so
|sin(a_n)|<|a_n|
Consider f(x) = x - sinx, we show f(x) > 0 (for x > 0)
Clearly f'(x) >= 0. When f'(x) = 0, we have x = 0 => f(x) = 0, or we have f(x) = 2npi - 0 > 0, and f(x) is increasing on all intervals between, easy to see that f(x) > 0
Then x > sin(x), since sin(x) AND x are odd we have |x| > |sinx| and so
|sin(a_n)|<|a_n|
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Sure, will do so tonight.Ah well, can you post the solution soon if no one gets it?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
For example, we could have a situation like 3->71->46->3 for student 3. This would mean that in the same arrangement of boxes, student 71 would follow this pattern: 71->46->3->71. What about students not in this "cycle"? They will be part of their own cycle. In this way, we can represent the way in which the numbered pieces of paper are placed in boxes as a number of disjoint (not containing any number in common) cycles. If each cycle corresponding to a given arrangement of numbered pieces of paper is of length 50 or less, then every student will traverse their full cycle and find their name. If even a single cycle of length > 50 exists, then the strategy will fail, as students in this cycle will not find their name.
So:
P(strat succeeds) = 1 - P(there exists a cycle of length > 50).
We can directly count the number of arrangements of numbered pieces of paper such that there is a cycle of length j for each j > 50 (out of the total 100! arrangements), which ends up giving us P(there is a cycle of length j) = 1/j for each j > 50 (do this yourself, it is similar to counting circular table arrangements).
Hence P(strat. succeeds) = 1 - 1/51 - 1/52 - ... - 1/100 = (approx.) 0.312.
My approximation was just from wolfram alpha, but you can approximate the sum quite accurately using integration to bound it between two logs.
So, the probability that this strategy leads to survival for the students is approximately 31%, which is REALLY good considering that if each student chooses randomly, there is a (1/2)^100 chance of survival!
If each student was allowed to open boxes indefinitely, as directed by the contained pieces of paper, he would eventually have to open a box he already has opened (as there are only finitely many boxes). As each box can only have one piece of paper pointing to it, this means that the box he has already opened must be the first box he opened, ie box k for student k.Ah well, can you post the solution soon if no one gets it?
For example, we could have a situation like 3->71->46->3 for student 3. This would mean that in the same arrangement of boxes, student 71 would follow this pattern: 71->46->3->71. What about students not in this "cycle"? They will be part of their own cycle. In this way, we can represent the way in which the numbered pieces of paper are placed in boxes as a number of disjoint (not containing any number in common) cycles. If each cycle corresponding to a given arrangement of numbered pieces of paper is of length 50 or less, then every student will traverse their full cycle and find their name. If even a single cycle of length > 50 exists, then the strategy will fail, as students in this cycle will not find their name.
So:
P(strat succeeds) = 1 - P(there exists a cycle of length > 50).
We can directly count the number of arrangements of numbered pieces of paper such that there is a cycle of length j for each j > 50 (out of the total 100! arrangements), which ends up giving us P(there is a cycle of length j) = 1/j for each j > 50 (do this yourself, it is similar to counting circular table arrangements).
Hence P(strat. succeeds) = 1 - 1/51 - 1/52 - ... - 1/100 = (approx.) 0.312.
My approximation was just from wolfram alpha, but you can approximate the sum quite accurately using integration to bound it between two logs.
So, the probability that this strategy leads to survival for the students is approximately 31%, which is REALLY good considering that if each student chooses randomly, there is a (1/2)^100 chance of survival!
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Pretty amazing how that strategy increases probability by a lot though....
=====
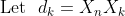

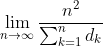
Oh I see, my answer was way off.If each student was allowed to open boxes indefinitely, as directed by the contained pieces of paper, he would eventually have to open a box he already has opened (as there are only finitely many boxes). As each box can only have one piece of paper pointing to it, this means that the box he has already opened must be the first box he opened, ie box k for student k.
For example, we could have a situation like 3->71->46->3 for student 3. This would mean that in the same arrangement of boxes, student 71 would follow this pattern: 71->46->3->71. What about students not in this "cycle"? They will be part of their own cycle. In this way, we can represent the way in which the numbered pieces of paper are placed in boxes as a number of disjoint (not containing any number in common) cycles. If each cycle corresponding to a given arrangement of numbered pieces of paper is of length 50 or less, then every student will traverse their full cycle and find their name. If even a single cycle of length > 50 exists, then the strategy will fail, as students in this cycle will not find their name.
So:
P(strat succeeds) = 1 - P(there exists a cycle of length > 50).
We can directly count the number of arrangements of numbered pieces of paper such that there is a cycle of length j for each j > 50 (out of the total 100! arrangements), which ends up giving us P(there is a cycle of length j) = 1/j for each j > 50 (do this yourself, it is similar to counting circular table arrangements).
Hence P(strat. succeeds) = 1 - 1/51 - 1/52 - ... - 1/100 = (approx.) 0.312.
My approximation was just from wolfram alpha, but you can approximate the sum quite accurately using integration to bound it between two logs.
So, the probability that this strategy leads to survival for the students is approximately 31%, which is REALLY good considering that if each student chooses randomly, there is a (1/2)^100 chance of survival!
Pretty amazing how that strategy increases probability by a lot though....
=====
- Status
- Not open for further replies.
