HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Alright, fresh start... sorry
Beginning from the use of induction hypothesis
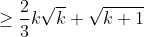
)
Now we need to prove that (time for a discovery)
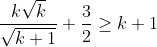
Subtract 1.5 on both sides
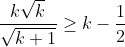
Multiply both sides by 2sqrt(k+1)
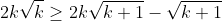
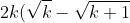 + \sqrt{k+1} \geq 0)
Edits:
Actually.. as k>0 and sqrt(k+1)>0, then sqrt(k) - sqrt(k+1)> 0 for LHS >0, so k>k+1, 0>1..................
When does equality occur?
Beginning from the use of induction hypothesis
Now we need to prove that (time for a discovery)
Subtract 1.5 on both sides
Multiply both sides by 2sqrt(k+1)
Edits:
Actually.. as k>0 and sqrt(k+1)>0, then sqrt(k) - sqrt(k+1)> 0 for LHS >0, so k>k+1, 0>1..................
When does equality occur?
Last edited:
