FrankXie
Active Member
Re: HSC 2015 4U Marathon
NEXT QUESTION
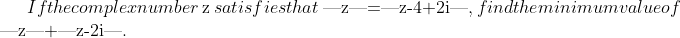
NEXT QUESTION
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Here's my go:NEXT QUESTION
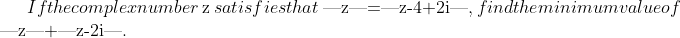
Geometry beats algebraHere's my go:
√(x^2 + y^2) = √[(x-4)^2 + (y+2)^2]
Simplification gives:
y = 2x - 5
|z| + |z - 2i| => |2z - 2i| = 2|z - i| (triangle inequality)
Clearly, equality is reached when x = 0
Sub x=0 into y = 2x - 5 = 2*0 - 5 = -5.
|-5| + |-5i+2i| = |-5| + |-3i| = 5 + 3 = 8.
I feel like my third last line ('clearly, equality...') is not very (for want of a better word) good. I tried solving it algebraically but I got nowhere, I just ended up with three square root terms, which, if x = 0 is subbed in, produces a correct result, however it just looked like a big mess. Is there a better way?
Oh my goodness, I'm stupid. Yes, I made the mistake that it was from (0,-2) not (0,2)hmm I am not sure whether that's right consider whether |z| lies on the
x-axis.
You get |z| = 2.5??
|z-2i| approx. 3 point something
which is less than 8 when added together.
|z-2i| is the distance from (0,2) to line not (0,-2)
so you actually consider the distance between
the line Y=2X+5 and (0,0)
and (0,2) added together
Let P(z) = iz^2 + (ia-1)z + (i-b)Find the values that the real numbers a and b can take for z=1 to be a root of the complex equation: iz^2+(ia-1)z+(i-b)=0
(starting easy as i'm not sure if everyone has begun the polynomials topic)
Note: Doesn't require '4U polynomial' knowledge
OMG THETA caps(sinθ - icosθ)^-8 = 1/(i(cosθ+isinθ))^8
(then by DeMoivre's theorem) = 1/(cos8θ+isin8θ)
LetLet P(x) be a polynomial with degree of 1996. If P(n) = 1/n for n = 1,2,3...1997, Find the value of P(1998)
Edit: Not sure if it is technically under the 4U syllabus, so just ignore it(By all means, try it if you wish)
Yep, slight error.so since A.B.Y are the roots of x^3 + 3x^2 - 4x + 5 = 0, then: A,B,Y are values of x
-> Rearranging: x^3=-3x^2 +4x -5
so, A^3 + B^3 + Y^3 = -3A^2 +4A -5 - 3B^2 +4B -5 - 3C^2 +4C -5 = -3(A^2+B^2+C^2) +4(A+B+C) -15
->A^2+B^2+C^2 = (A+B+Y)^2 - 2(AB +BC +AC) = 1
-
therefore A^3 + B^3 + Y^3 = -3(1) +4(-3) -15
=-30
(Prob mistake somewhere, hella hard to type in this shifty font)
wallah im stoned on chocolatesYep, slight error.
AB+AC+BC = -4
So A^2+B^2+C^2 = 3^2 -2(-4) = 17
good try but i'm afraid it is invalid.Here's my go:
√(x^2 + y^2) = √[(x-4)^2 + (y+2)^2]
Simplification gives:
y = 2x - 5
|z| + |z - 2i| => |2z - 2i| = 2|z - i| (triangle inequality)
Clearly, equality is reached when x = 0
Sub x=0 into y = 2x - 5 = 2*0 - 5 = -5.
|-5| + |-5i+2i| = |-5| + |-3i| = 5 + 3 = 8.
I feel like my third last line ('clearly, equality...') is not very (for want of a better word) good. I tried solving it algebraically but I got nowhere, I just ended up with three square root terms, which, if x = 0 is subbed in, produces a correct result, however it just looked like a big mess. Is there a better way?
