Okay guys noone helped I seriously need help. And what does mif mean?
Draw a diagram like this: draw two parallel horizontal lines. Put a point labelled
P on one line (this is where the man starts), and a point
A directly opposite on the other horizontal line (this is the shore), so that
PA = 6 km. Put point
B on the same horizontal line as
A, 20 km to the right, so
AB = 20 km, and note that
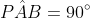
.
Label a point
X between
A and
B, and let the distance
AX be
x km (so
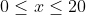
). This is how far from
A he lands. We seek to find the
x that minimises the time taken.
From the diagram, you see that he rows the length
PX and runs the length
XB. From triangle
PAX, Pythagoras' Theorem gives us
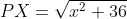
. Also, clearly
XB = 20 –
x.
His time in hours to row
PX is
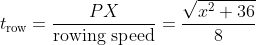
, since time = distance/speed.
Similarly, time to run
BX is
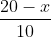
.
So his total time taken is
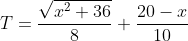
.
Now we have the total time required as a function of
x, so we can optimise
T.
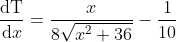
.
Set the derivative to 0 to find minimal time:
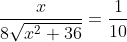
}=\frac{1}{100})
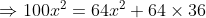
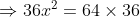
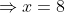
(since
x > 0).
Remember to test this to show it gives the minimal time (this can be shown by noting that the derivative
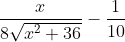
is less than 0 when
x is just less than 8, and that it's greater than 0 when
x is just greater than 8, so
x = 8 gives the minimum).
So the answer is 8 km.
