Area under curve (Trigonometric functions) (1 Viewer)

[BlueGas]

Find the area under the curve y = 3cosx + 4sinx between x = 0 and x = Pi/4

 

[InteGrand]

Find the area under the curve y = 3cosx + 4sinx between x = 0 and x = Pi/4

Have you tried sketching the graph? To do this, we find for what value(s) of x in the interval from 0 to the function is 0, and find the values at the endpoints, and then draw a rough shape.

 

[BlueGas]

Have you tried sketching the graph? To do this, we find for what value(s) of x in the interval from 0 to the function is 0, and find the values at the endpoints, and then draw a rough shape.

I don't know how to sketch these sort of graphs, my teacher skipped that part (sketching) and I'm not sure when we're going to go over this. I've done other questions without sketching and got the right answer, but it seems I need to sketch for this one.

 

[InteGrand]

I don't know how to sketch these sort of graphs, my teacher skipped that part (sketching) and I'm not sure when we're going to go over this. I've done other questions without sketching and got the right answer, but it seems I need to sketch for this one.

In this case, the function turns out to be always positive in the given domain, so the area is just given by .

 

[InteGrand]

Here's how to see the function is always positive in the given domain:

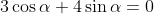
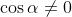
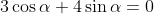
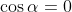
If , then dividing through by cos α (which we can do because we know for , because if , then sin α equals either 1 or -1, and neither of these makes )

.

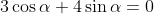
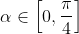
This is not true for any , since the tan function is positive or 0 in this domain. So the function never crosses the y-axis in this domain.

So we just need to see whether the function's graph is above, or below, the y-axis. We find that at x = 0, the function equals 3, which is positive. So the function's graph is always above the x-axis in the domain of integration (i.e. function always positive here, so the integral also gives us the area under the curve).