-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Integration Marathon (archive) (2 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
EDIT: and not so sure about the bionomial coefficients that you had ?
There should be 1/(n-k)! due to the partial fractions coefficients change(-1)^k is the same as (-1)^(2+k)
The expression looks decent. I can't be bothered figuring out my combinatorics right now, but I found this:
 { \left( -1 \right) }^{ k }\ln { \left| x+k \right| } } )
EDIT: and not so sure about the bionomial coefficients that you had ?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
I suppose, if the binomial coefficients were expanded I'd have ended up with a 1/(k!) * 1/(n-k)!
I checked on Wolfram Alpha and I realised that the terms followed Pascal's triangle, which was what lead me to the assumption of the binomial coefficient being related.
 =\frac { n! }{ k!\left( n-k \right) ! } )
The binomial coefficients spit out a 1/(n-k)! quantity anyway.There should be 1/(n-k)! due to the partial fractions coefficients change
EDIT: and not so sure about the bionomial coefficients that you had ?
I suppose, if the binomial coefficients were expanded I'd have ended up with a 1/(k!) * 1/(n-k)!
I checked on Wolfram Alpha and I realised that the terms followed Pascal's triangle, which was what lead me to the assumption of the binomial coefficient being related.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
hmmmm... what method did you useThe binomial coefficients spit out a 1/(n-k)! quantity anyway.
I suppose, if the binomial coefficients were expanded I'd have ended up with a 1/(k!) * 1/(n-k)!
I checked on Wolfram Alpha and I realised that the terms followed Pascal's triangle, which was what lead me to the assumption of the binomial coefficient being related.
 =\frac { n! }{ k!\left( n-k \right) ! } )
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Partial fractions on n=0, 1, 2, 3 then I checked them on WolframAlpha. Didn't realise a pattern with the binomial coefficients until I saw the Mathematica solutions though. Then I just plugged n=4 and n=5 in and it turned out to be the same. I couldn't be bothered doing over n=3
Partial fractions on n=0, 1, 2, 3 then I checked them on WolframAlpha. Didn't realise a pattern with the binomial coefficients until I saw the Mathematica solutions though. Then I just plugged n=4 and n=5 in and it turned out to be the same. I couldn't be bothered doing over n=3
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
(2)...(n)} )
!} )
} )
yeah i did the samePartial fractions on n=0, 1, 2, 3 then I checked them on WolframAlpha. Didn't realise a pattern with the binomial coefficients until they put it up though. Then I just plugged n=4 and n=5 in and it turned out to be the same. I couldn't be bothered doing over n=3
Re: MX2 2015 Integration Marathon
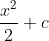
Oh whoops I forgot a +C...
---------------
Have a break.
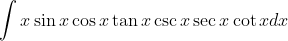
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
}dx )
Re: MX2 2015 Integration Marathon
Can't do it with elementary functions
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Just asking out of curiosity, do you make up integrals on the spot Drsoccerball? When I do that I usually plug them into mathematica or something to make sure they work. Friendly advice
---------------------------

Just asking out of curiosity, do you make up integrals on the spot Drsoccerball? When I do that I usually plug them into mathematica or something to make sure they work. Friendly advice
---------------------------
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
I_{n-2}}{n-1} )

The reduction formula is:Just asking out of curiosity, do you make up integrals on the spot Drsoccerball? When I do that I usually plug them into mathematica or something to make sure they work. Friendly advice
---------------------------

Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,612
- Gender
- Male
- HSC
- 2015
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,612
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Integral is positive and comes out to be something interesting, as found by a quite tedious computation (involving polynomial division etc.).
Last edited:
- Status
- Not open for further replies.
