Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Permutations & Combinations Marathon (archive) (1 Viewer)
- Thread starter Drsoccerball
- Start date
- Status
- Not open for further replies.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon
1/2 ? It doesn't matter if he switches.
Re: 2015 permutation X2 marathon
Something that is interesting about the Monty Hall problem (assuming the host always reveals a goat, so the probabilities are 1/3 and 2/3):
If someone walks onto the set after the host has opened a door (so he doesn't know the player's original choice) and bets on the location of the car, it will be a 50-50 bet for him.
So each person will have a different probability for each door, yet BOTH sets of probabilities will be borne out by repeated trials.
Something that is interesting about the Monty Hall problem (assuming the host always reveals a goat, so the probabilities are 1/3 and 2/3):
If someone walks onto the set after the host has opened a door (so he doesn't know the player's original choice) and bets on the location of the car, it will be a 50-50 bet for him.
So each person will have a different probability for each door, yet BOTH sets of probabilities will be borne out by repeated trials.
Re: 2015 permutation X2 marathon
Yep. The knowledge of the observer is everything.Something that is interesting about the Monty Hall problem (assuming the host always reveals a goat, so the probabilities are 1/3 and 2/3):
If someone walks onto the set after the host has opened a door (so he doesn't know the player's original choice) and bets on the location of the car, it will be a 50-50 bet for him.
So each person will have a different probability for each door, yet BOTH sets of probabilities will be borne out by repeated trials.
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon
Are these all similar to the "not looking" pick from a bag full of marbles ?
Are these all similar to the "not looking" pick from a bag full of marbles ?
Re: 2015 permutation X2 marathon
Aren't all picks "not looking"? It is hard to pick randomly if you look.Are these all similar to the "not looking" pick from a bag full of marbles ?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon
No like the resulting marbles. If I don't look at put it back vs if i look then put it back.Aren't all picks "not looking"? It is hard to pick randomly if you look.
Silly Sausage
Well-Known Member
- Joined
- Dec 8, 2014
- Messages
- 594
- Gender
- Male
- HSC
- 2014
Re: 2015 permutation X2 marathon
You can think of it as this way: If the player picks the door with the goat initially=\frac{1}{3}) and switches, his chances of winning the goat is 100%. Since the probabilities of which of the two doors with the car behind it do NOT change and that the player does know which door the car is behind, the probability of winning the car is
and switches, his chances of winning the goat is 100%. Since the probabilities of which of the two doors with the car behind it do NOT change and that the player does know which door the car is behind, the probability of winning the car is 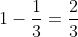 . If he doesn't switch his chances of winning the car is obviously
. If he doesn't switch his chances of winning the car is obviously  .
.
You can think of it as this way: If the player picks the door with the goat initially
Re: 2015 permutation X2 marathon
This was how I used to think of it (and still do mostly), but the problem with it is that I don't think it really explains the case where Monty picks the doors randomly and happens to show a goat.You can think of it as this way: If the player picks the door with the goat initiallyand switches, his chances of winning the goat is 100%. Since the probabilities of which of the two doors with the car behind it do NOT change and that the player does know which door the car is behind, the probability of winning the car is
. If he doesn't switch his chances of winning the car is obviously
.
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Re: 2015 permutation X2 marathon
Fred lives on one of 10 islands sitting in a vast lake. One day a package drops uniformly at random on one of the ten islands. Fred can't swim and has no boat, but luckily there is a teleporter on each island. Each teleporter teleports to only one of the other ten teleporters (note that it may teleport to itself), and no two teleporters teleport to the same teleporter. If the configuration of the teleporters is chosen uniformly at random from all configurations that satisfy these constraints, compute the probability that Fred can get to the package using the teleporters.
Answer: 11/20
Fred lives on one of 10 islands sitting in a vast lake. One day a package drops uniformly at random on one of the ten islands. Fred can't swim and has no boat, but luckily there is a teleporter on each island. Each teleporter teleports to only one of the other ten teleporters (note that it may teleport to itself), and no two teleporters teleport to the same teleporter. If the configuration of the teleporters is chosen uniformly at random from all configurations that satisfy these constraints, compute the probability that Fred can get to the package using the teleporters.
Answer: 11/20
Re: 2015 permutation X2 marathon
working: 0.1 + 0.9/(9*10) * (1 + 2 +...+9)
basically i counted permutations l0l
OK well i got 55% is that right hahaha (assuming that not using a teleporter counts as 'using the teleporters')Fred lives on one of 10 islands sitting in a vast lake. One day a package drops uniformly at random on one of the ten islands. Fred can't swim and has no boat, but luckily there is a teleporter on each island. Each teleporter teleports to only one of the other ten teleporters (note that it may teleport to itself), and no two teleporters teleport to the same teleporter. If the configuration of the teleporters is chosen uniformly at random from all configurations that satisfy these constraints, compute the probability that Fred can get to the package using the teleporters.
Answer: 11/20
working: 0.1 + 0.9/(9*10) * (1 + 2 +...+9)
basically i counted permutations l0l
Last edited:
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Re: 2015 permutation X2 marathon
Yep that's the correct answer. I'm guessing the 0.1 is if it lands on the island he is on. Can you explain the second part?OK well i got 55% is that right hahaha (assuming that not using a teleporter counts as 'using the teleporters')
working: 0.1 + 0.9/(9*10) * (1 + 2 +...+9)
basically i counted permutations l0l
Re: 2015 permutation X2 marathon
SWEET yeah 0.1 is if he lands on the island he's on.
Ok, my explaining skills are actually pretty shit, but here goes.
I numbered the islands from 0 to 9
and then i made a 10 digit number, where first digit is the island that the teleporter on 0 is directed to, 2nd digit is the island that island 1's teleporter goes to
eg. 9876543210
teleporter on 0 is directed to 9
So then, I let the dude start on island 0, and the randomly dropped gift go on island 1 (by symmetry it doesn't matter)
I counted the permutations that were valid, and divided by total permutations
now let's consider a 'chain', which is a cycle of islands that the guy can cycle through. if the situation was 1023456789, then the guy would continually cycle between 0 and 1, so this is a cycle of length 2, and 1203456789 would be a cycle length 3 (cycling through 0, 1, 2)
so consider a cycle of length k, and count the valid permutations provided 0 and 1 are linked in a chain
We pick the k-2 remaining members of the chain
8C(k-2)
We permute them, however noting that a chain 123 is equivalent as chain 231 (sorta a circular thing) BUT different to 213
k! / k
now we permute the remaining 10-k items
(10-k)!
and divide by total perms
10!
so we got
8C(k-2)*(k-1)!(10-k)! / 10!
simplifying to (k-1)/90
so then sum up k= 2, 3, 4, 5, ... 10
and you get (1 + 2 +...+9)
NOW PUTTING THE PIECES TOGETHER
you got 0.1 chance for landing on the island he's on
0.9 for not landing on the island he is on
within the 0.9 you got the probabilty of (1+2+..+9) / 90
hence the answer 0.1 + 0.9/(9*10) * (1 + 2 +...+9) = 0.55
SWEET yeah 0.1 is if he lands on the island he's on.
Ok, my explaining skills are actually pretty shit, but here goes.
I numbered the islands from 0 to 9
and then i made a 10 digit number, where first digit is the island that the teleporter on 0 is directed to, 2nd digit is the island that island 1's teleporter goes to
eg. 9876543210
teleporter on 0 is directed to 9
So then, I let the dude start on island 0, and the randomly dropped gift go on island 1 (by symmetry it doesn't matter)
I counted the permutations that were valid, and divided by total permutations
now let's consider a 'chain', which is a cycle of islands that the guy can cycle through. if the situation was 1023456789, then the guy would continually cycle between 0 and 1, so this is a cycle of length 2, and 1203456789 would be a cycle length 3 (cycling through 0, 1, 2)
so consider a cycle of length k, and count the valid permutations provided 0 and 1 are linked in a chain
We pick the k-2 remaining members of the chain
8C(k-2)
We permute them, however noting that a chain 123 is equivalent as chain 231 (sorta a circular thing) BUT different to 213
k! / k
now we permute the remaining 10-k items
(10-k)!
and divide by total perms
10!
so we got
8C(k-2)*(k-1)!(10-k)! / 10!
simplifying to (k-1)/90
so then sum up k= 2, 3, 4, 5, ... 10
and you get (1 + 2 +...+9)
NOW PUTTING THE PIECES TOGETHER
you got 0.1 chance for landing on the island he's on
0.9 for not landing on the island he is on
within the 0.9 you got the probabilty of (1+2+..+9) / 90
hence the answer 0.1 + 0.9/(9*10) * (1 + 2 +...+9) = 0.55
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon

Answer: 11/50
Answer: 11/50
RealiseNothing
what is that?It is Cowpea
Re: 2015 permutation X2 marathon
Two people play a game (call them A and B).
1. Numbers between 1 and 30 inclusive are written on balls and put in a bag.
2. Person A chooses a number, then person B chooses a number.
3. A ball is then drawn.
The closest person to the number drawn wins an amount equal to the number drawn in dollars. Eg. If A chooses 10, B chooses 20, and 16 is drawn, then B wins $16.
Suppose A and B both play optimally, what numbers do A and B choose?
Two people play a game (call them A and B).
1. Numbers between 1 and 30 inclusive are written on balls and put in a bag.
2. Person A chooses a number, then person B chooses a number.
3. A ball is then drawn.
The closest person to the number drawn wins an amount equal to the number drawn in dollars. Eg. If A chooses 10, B chooses 20, and 16 is drawn, then B wins $16.
Suppose A and B both play optimally, what numbers do A and B choose?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon
LOL 30 so they both get $30Two people play a game (call them A and B).
1. Numbers between 1 and 30 inclusive are written on balls and put in a bag.
2. Person A chooses a number, then person B chooses a number.
3. A ball is then drawn.
The closest person to the number drawn wins an amount equal to the number drawn in dollars. Eg. If A chooses 10, B chooses 20, and 16 is drawn, then B wins $16.
Suppose A and B both play optimally, what numbers do A and B choose?
Re: 2015 permutation X2 marathon
Don't think they're allowed to choose the same number. (And the money the winner gets is the number drawn from the bag.)LOL 30 so they both get $30
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: 2015 permutation X2 marathon
Well if they play wouldn't one pick 1 and the other picks 30?Don't think they're allowed to choose the same number. (And the money the winner gets is the number drawn from the bag.)
Re: 2015 permutation X2 marathon
No, doubt it.Well if they play wouldn't one pick 1 and the other picks 30?
- Status
- Not open for further replies.
