-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2016 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Re: HSC 2016 4U Marathon
. For upwards motion, it is generally more convenient to have the positive direction be upwards, so the weight force would point in the negative direction (as it points down). This would make the weight force vector be $\overrightarrow {W} = -mg$, where $g$ is a \textsl{positive} quantity (that's why we need the minus sign here).$)
, and so the weight vector is $\overrightarrow{W} = mg$, where $g$ is a positive quantity.$)
When I did mechanics, and I had to resolve forces in upwards motion, I used -g.
When I had downwards motion, I took +g.
That is all I will say
Re: HSC 2016 4U Marathon
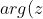-arg(z+i)=\frac{5\pi}{4}\\\tan^{-1}(\frac{y}{x})-\tan^{-1}(\frac{y+1}{x}) = \frac{5\pi}{4}\\\frac{y}{x}-\frac{y+1}{x}=1\\y-y-1=x\\x=-1)
I'm 90% sure this is wrong. If you could tell me what's wrong about it, that would be great. I can't even picture this locus in my head. It's a weird one.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 4U Marathon
But wait for some experienced person to explain to you THAT locus
Line 3: You didn't use compound angles.I'm 90% sure this is wrong. If you could tell me what's wrong about it, that would be great. I can't even picture this locus in my head. It's a weird one.
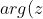-arg(z+i)=\frac{5\pi}{4}\\\tan^{-1}(\frac{y}{x})-\tan^{-1}(\frac{y+1}{x}) = \frac{5\pi}{4}\\\frac{y}{x}-\frac{y+1}{x}=1\\y-y-1=x\\x=-1)
But wait for some experienced person to explain to you THAT locus
Re: HSC 2016 4U Marathon
 \neq \tan^{-1} \left( \frac{y}{x}\right)$ (that equality is true if and only if $x>0$), where $x$ and $y$ are the real and imaginary parts of $\omega$, respectively. It is always true though that if $x\neq 0$, then $\tan \left(\arg \left(\omega\right) \right) =\frac{y}{x}$.$)
I'm 90% sure this is wrong. If you could tell me what's wrong about it, that would be great. I can't even picture this locus in my head. It's a weird one.
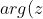-arg(z+i)=\frac{5\pi}{4}\\\tan^{-1}(\frac{y}{x})-\tan^{-1}(\frac{y+1}{x}) = \frac{5\pi}{4}\\\frac{y}{x}-\frac{y+1}{x}=1\\y-y-1=x\\x=-1)
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
The locus for the original question would be the major arc of a circle with centre to the left of the y axis with the angle between vectors z+i and z being 5pi/4I'm 90% sure this is wrong. If you could tell me what's wrong about it, that would be great. I can't even picture this locus in my head. It's a weird one.
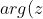-arg(z+i)=\frac{5\pi}{4}\\\tan^{-1}(\frac{y}{x})-\tan^{-1}(\frac{y+1}{x}) = \frac{5\pi}{4}\\\frac{y}{x}-\frac{y+1}{x}=1\\y-y-1=x\\x=-1)
Last edited:
appleibeats
Member
- Joined
- Oct 30, 2012
- Messages
- 375
- Gender
- Male
- HSC
- 2016
Re: HSC 2016 4U Marathon
determine the arcs specified by the following eqn. Sketch each one, showing the centre and radius of the associated circle.
arg ( z - 1 + i) / (z - 1 - i ) = pi/2
So i know it a circle. there are endpoints at (1, -1 ) and ( 1, 1) and that there are not included , hollow dot.
The angle between these two vectors when they meet is pi /2 .
The answers say it is a right hand side semicircle. Why is it a semicircle and not a full circle??
determine the arcs specified by the following eqn. Sketch each one, showing the centre and radius of the associated circle.
arg ( z - 1 + i) / (z - 1 - i ) = pi/2
So i know it a circle. there are endpoints at (1, -1 ) and ( 1, 1) and that there are not included , hollow dot.
The angle between these two vectors when they meet is pi /2 .
The answers say it is a right hand side semicircle. Why is it a semicircle and not a full circle??
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
Draw up the vectors. Remember that anti-clockwise angles are positive. Drawing the left hand side semicircle and the vectors, the angle between them will be -pi/2 not pi/2 so you can only accept the right and side.determine the arcs specified by the following eqn. Sketch each one, showing the centre and radius of the associated circle.
arg ( z - 1 + i) / (z - 1 - i ) = pi/2
So i know it a circle. there are endpoints at (1, -1 ) and ( 1, 1) and that there are not included , hollow dot.
The angle between these two vectors when they meet is pi /2 .
The answers say it is a right hand side semicircle. Why is it a semicircle and not a full circle??
Re: HSC 2016 4U Marathon
= \alpha$ for a given $\alpha \in \left(0,\pi\right)$ is to start at the point $z_1$ and go counter-clockwise in a circular arc to the point $z_2$, with an angle of $\alpha$ being subtended in this arc (with open circles at $z_1$ and $z_2$, that is, these points are excluded from the locus). If you have the \textsl{other} arc, this corresponds to the locus $\arg \left(\frac{z -z_2}{z -z_1}\right)=\alpha$.$)
determine the arcs specified by the following eqn. Sketch each one, showing the centre and radius of the associated circle.
arg ( z - 1 + i) / (z - 1 - i ) = pi/2
So i know it a circle. there are endpoints at (1, -1 ) and ( 1, 1) and that there are not included , hollow dot.
The angle between these two vectors when they meet is pi /2 .
The answers say it is a right hand side semicircle. Why is it a semicircle and not a full circle??
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon


Attachments
-
6.8 KB Views: 125
Re: HSC 2016 4U Marathon
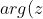\neq arg(z)+2\pi) as adding
as adding 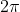 to one side fundamentally changes the value. Take for example
to one side fundamentally changes the value. Take for example
=\frac{\pi}{4}\\arg(z)+2\pi=\frac{\pi}{4}+2\pi=\frac{9\pi}{4}\\\frac{\pi}{4}\neq\frac{9\pi}{4})
Adding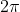 to the argument of a complex number will rotate the complex number a full revolution around the origin and will result in the same number. Finding the argument of a complex number and then adding
to the argument of a complex number will rotate the complex number a full revolution around the origin and will result in the same number. Finding the argument of a complex number and then adding 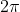 to that is not the same as the argument of the original complex number.
to that is not the same as the argument of the original complex number.
NEXT QUESTION: Using De Moivre's theorem, prove that
arg(z) refers to the angle created by the line from the origin to the complex number z and the positive real axis on the Argand diagram.
Adding
NEXT QUESTION: Using De Moivre's theorem, prove that
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
 )
NEXT QUESTION: Using De Moivre's theorem, prove that
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 4U Marathon
Also, something tells me you made an assumption that |z|=1
Correcting your question. If my mental arithmetic is correct, the answer is actually 2 * cos(ntheta)What?
Also, something tells me you made an assumption that |z|=1
appleibeats
Member
- Joined
- Oct 30, 2012
- Messages
- 375
- Gender
- Male
- HSC
- 2016
Re: HSC 2016 4U Marathon
why is arg( (z)^1/2) = 1/2 arg z
why is arg( (z)^1/2) = 1/2 arg z
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 4U Marathon
When z=cos(x)+isin(x)
z^n = (cos(x)+isin(x))^n = cos(nx)+isin(nx)
arg(LHS) = arg(z^n)
Take note arg(z)=x
arg(RHS)=nx
So arg(z^n)=nx
arg(z^n)=n*arg(z)
That's just the case when n=1/2 (NOTE: N ACTUALLY DOES NOT HAVE TO BE AN INTEGER. It's only called De Moivre's theorem when we deal with positive integers that's all. the statement is actually true for all real n)
De Moivre's theorem stateswhy is arg( (z)^1/2) = 1/2 arg z
When z=cos(x)+isin(x)
z^n = (cos(x)+isin(x))^n = cos(nx)+isin(nx)
arg(LHS) = arg(z^n)
Take note arg(z)=x
arg(RHS)=nx
So arg(z^n)=nx
arg(z^n)=n*arg(z)
That's just the case when n=1/2 (NOTE: N ACTUALLY DOES NOT HAVE TO BE AN INTEGER. It's only called De Moivre's theorem when we deal with positive integers that's all. the statement is actually true for all real n)
- Status
- Not open for further replies.

