Continuing off of what I just talked about, the Heegner numbers are connected to the quadratic polynomial:
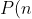 \equiv n^2 + n + 41)
This polynomial outputs distinct prime numbers for the numbers 0 to 39
The generalised quadratic equation:
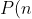 \equiv n^2 + n + p)
will also output distinct primes for the numbers 0 to p-2, if and only if, the discriminant of 1-4p is equal to a Heegner number.
Unfortunately, due to the fact that there are only a finite number of Heegner numbers, there are only a finite number of quadratic equations with this beautiful property. Specifically, only 6 of the 9 Heegner numbers have this property.
