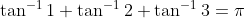HSC 2016 MX2 Complex Numbers Marathon (archive) (3 Viewers)

porcupinetree · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

tywebb said:
Better still, prove that

$x>\textstyle\sqrt{y^2+1}\Rightarrow\tan^{-1}(x-y)+\tan^{-1}(x+y)+\tan^{-1}\frac{2x}{x^2-y^2-1}=\pi$

and hence if x=2 and y=1 then

$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3=\pi$

I don't like my proof for this; it seems too convoluted

Ceebs finding a more elegant proof tho

Paradoxica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

porcupinetree said:
I don't like my proof for this; it seems too convoluted

Ceebs finding a more elegant proof tho

The expected proof is assisted greatly using a geometric representation of the situation.

math man · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

porcupinetree said:
I don't like my proof for this; it seems too convoluted

Ceebs finding a more elegant proof tho

Use same method to prove it as paradoxica did above with complex numbers.

KingOfActing · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

porcupinetree said:
I don't like my proof for this; it seems too convoluted

Ceebs finding a more elegant proof tho

The way I thought to go about it was just to consider the product (1+(x-y)i)(1+(x+y)i)(x^2-y^2-1+2xi) similar to the way (1+i)(1+2i)(1+3i) was used in the easier question. Then the only identity you need is arg(abc) = arg(a) + arg(b) + arg(c)

edit: yup what math man said

Unravel · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

porcupinetree said:
I don't like my proof for this; it seems too convoluted

Ceebs finding a more elegant proof tho

The complex numbers method by considering the arg of (1+(x-y)i)(1+(x+y)i)(1+2x/(x^2-y^2-1)i) is more elegant, there are a few tricks to handle the expansion quickly

Edit: Lol beaten by the above two people

Paradoxica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

math man said:
Use same method to prove it as paradoxica did above with complex numbers.

that's terrible.

Paradoxica

parad0xica

you should really discern the two, I'll forgive this time around because it's obvious if people scroll up.

porcupinetree · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

Paradoxica said:
that's terrible.

Paradoxica

parad0xica

you should really discern the two, I'll forgive this time around because it's obvious if people scroll up.

Don't forget paradixica

leehuan · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

Who is Parad0xica

InteGrand · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

leehuan said:
Who is Parad0xica

There is no Parad0xica, there is only parad0xica and Paradoxica (I'm getting that effect now where if you say a word too many times it seems to lose its meaning, where the word in question is "Paradoxica").

(Incidentally, this effect is known as semantic satiation and can be read about here: https://en.wikipedia.org/wiki/Semantic_satiation .)

Paradoxica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

InteGrand said:
There is no Parad0xica, there is only parad0xica and Paradoxica (I'm getting that effect now where if you say a word too many times it seems to lose its meaning, where the word in question is "Paradoxica").

semantic satiation... how I love/hate it.

parad0xica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

Highlight below to see answer. Alternatively, press (CTRL + a) to highlight the whole page which is quicker.

Consider (1 + i(x - y)) (1+ i(x + y)) (x² - y² - 1 + 2ix) and expanding

= (1 + 2ix - (x²) - y² - 1)) ((x² - y² - 1 + 2ix))

= -4x² - (x² - y² - 1)^2

= some negative real.

Now we use our first hypothesis:

x > √(y² + 1 (thus x >= 1) . . . (*)

x² > y² + 1

x² -y² > 1 . . . (**)

(x+y)(x-y) > 1

Consider the graph for (**), then for all x > 1, there is both +y and -y corresponding to each x and |y| does not exceed x otherwise hypothesis (*) is violated. That means we have (x + |y|) > 0.

That means the complex numbers (1 + i(x + y)) and (1+ i(x - y)) are either both in the 1st quadrant, by (***). Hence their arguments are arctan(x + y) and arctan(x - y) respectively.

By (*) and (**), we have that the complex number (x² - y² - 1 + 2ix) must lie in the first quadrant. Thus, we can use the arctan(b/a) formula to compute the argument.

It's time to run home. Take argument of both sides of the very first equation

arg((1 + i(x - y)) (1+ i(x + y)) (x² - y² - 1 + 2ix)) = arg(some negative real)

arg((1 + i(x - y)) + arg(1+ i(x + y)) + arg(x² - y² - 1 + 2ix)) = pi

arctan(x + y) + arctan(x - y) + arctan( 2x / (x² - y² - 1)) = pi

Lol, I was to slow...

parad0xica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

porcupinetree said:
Don't forget paradixica

Who is that? It's not me.

Last seen: Yesterday 3:16 PM

No activity since some liking of comments just over a week ago. What is their purpose and why aren't they doing anything? I'm thinking it's an alternate account to private message some people for some reasons...

tywebb · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

Paradoxica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

tywebb said:

As I have already asked, do you happen to have any additional magical (conditionally true) trigonometric identities?

InteGrand · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

Paradoxica said:
As I have already asked, do you happen to have any additional magical (conditionally true) trigonometric identities?

I'm guessing you've already memorised most of the ones on Wikipedia?

Paradoxica · Apr 18, 2016

Re: HSC 2016 Complex Numbers Marathon

InteGrand said:
I'm guessing you've already memorised most of the ones on Wikipedia?

The interesting ones. Which is highly subjective, but hey, it's my decision

math man · Apr 19, 2016

Re: HSC 2016 Complex Numbers Marathon

NEW
Q. Find tan(3 theta) in terms of tan(theta) using demovire theorem and binomial theorem.
Hence, find exact value of cot(pi/12).

Paradoxica · Apr 19, 2016

Re: HSC 2016 Complex Numbers Marathon

$$\noindent a) Show that, for any integer $n>0 \\ $\indent$ \prod_{r=1}^{n} 2\cos{\frac{r\pi}{2n+1}} =1 \\ $\indent by considering the roots of $ z^{2n+1} = 1 \\ $b) Hence, prove the following numerical identity:$ \\ $\indent$ \sum_{n=1}^{\infty} \prod_{r=1}^{n} \cos{\frac{r\pi}{2n+1}} = 1$

KingOfActing · Apr 19, 2016

Re: HSC 2016 Complex Numbers Marathon

math man said:
NEW
Q. Find tan(3 theta) in terms of tan(theta) using demovire theorem and binomial theorem.
Hence, find exact value of cot(pi/12).

$From de Moivre's formula: $\\\cos{3\theta} +i\sin3\theta = \cos^3\theta + 3i\cos^2{\theta}\sin\theta - 3\cos\theta\sin^2\theta - i\sin^3\theta\\$Hence:$
$\begin{align*} \tan{3\theta} &= \frac{\sin3\theta}{\cos3\theta} \\&= \frac{3\cos^2\theta\sin\theta - \sin^3\theta}{\cos^3\theta -3\cos\theta\sin^2\theta}\\&=\frac{3\tan\theta - \tan^3\theta}{1-3\tan^2\theta} \end{align*}$
$$In order to find $\cot{\frac{\pi}{12}}$, we proceed in the following way:$\\$Let $ c = \cot{\frac{\pi}{12}}\\\tan{3\theta} = \frac{3\cot^2{\theta} - 1}{\cot^3\theta - 3\cot\theta}\\1 = \frac{3c^2 - 1}{c^3-3c}\\c^3-3c^2-3c+1 = 0\\(c+1)(c^2-4c+1) = 0\\$Note that the cotangent function is strictly decreasing over $(0,\pi]$, hence:$\\ \frac{\pi}{4} > \frac{\pi}{12} \implies \cot{\frac{\pi}{4}} < c \\ 1 < c\\$The only solution for the cubic that satisfies this conidition is $ c = 2 + \sqrt{3}$

math man · Apr 20, 2016

Re: HSC 2016 Complex Numbers Marathon

Paradoxica said:
$$\noindent a) Show that, for any integer $n>0 \\ $\indent$ \prod_{r=1}^{n} 2\cos{\frac{r\pi}{2n+1}} =1 \\ $\indent by considering the roots of $ z^{2n+1} = 1 \\ $b) Hence, prove the following numerical identity:$ \\ $\indent$ \sum_{n=1}^{\infty} \prod_{r=1}^{n} \cos{\frac{r\pi}{2n+1}} = 1$

Bump! Someone should try this neat and elegant exercise

HSC 2016 MX2 Complex Numbers Marathon (archive) (3 Viewers)

not actually a porcupine

-insert title here-

Member

lukewarm mess

New Member

-insert title here-

not actually a porcupine

Well-Known Member

Well-Known Member

-insert title here-

Active Member

Active Member

dangerman

Attachments

-insert title here-

Well-Known Member

-insert title here-

Member

-insert title here-

lukewarm mess

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)