Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Do we need to memorise this identity? (1 Viewer)
- Thread starter SammyT123
- Start date
Which identity? You will need to leave the final answer in terms of x.Solving the following integral:
\\ $To simplify do I need the tan(x/2) = sqrt()/sqrt() result -->Cosine?$\\ $Any other way to do it?$)
For that integral, you could also use a trig. substitution of x = a*tan(theta).
You end up with something involving integral of cosec(theta), which is:
-ln(cosec(theta) + cot(theta)).
Then you could convert this back to in terms of x, using trig. identities or a right-angled triangle to assist you. This avoids use of tan(theta/2).
Last edited:
Sorry, I did substitute x=atan(theta)
Identity is give here
https://www.quora.com/How-could-one...ot-of-1-cosx-1+cosx-absolute-value-of-tan-x-2
Identity is give here
https://www.quora.com/How-could-one...ot-of-1-cosx-1+cosx-absolute-value-of-tan-x-2
So my qs is
put tan(theta/2) in terms of x where x=tan(theta)
This identity isn't expected to be memorised for the HSC, but you should be able to derive it if needed.
Could derive it, but imagine me sitting in the 4U trials thinking
This identity isn't expected to be memorised for the HSC, but you should be able to derive it if needed.
x=tan(theta)
t=tan(theta/2)
"Oh boy better derive that weird squareroot cosine formula!!"
haha so is there any clue in the question or solution that allows me to conclude that formula is needed
Assuming I do derive this in the exam, the integral is still quite tedious



Last edited:
Well we didn't need that formula to do that integral in the original post. We could avoid half-angles as I showed. But if you did introduce half-angles, the way to get out of them is to use the half-angle formulas in some way, because these formulas tell us how to go from sin(a/2) and cos(a/2) (and hence tan(a/2)) to trig functions of a. (That's how I derived that formula above.)Could derive it, but imagine me sitting in the 4U trials thinking
x=tan(theta)
t=tan(theta/2)
"Oh boy better derive that weird squareroot cosine formula!!"
haha so is there any clue in the question or solution that allows me to conclude that formula is needed
Seem to be gettingWhich identity? You will need to leave the fnal answer in terms of x.
For that integral, you could also use a trig. substitution of x = a*tan(theta).
You end up with something involving integral of cosec(theta), which is:
-ln(cosec(theta) + cot(theta)).
Then you could convert this back to in terms of x, using trig. identities or a right-angled triangle to assist you. This avoids use of tan(theta/2).
Any way I can avoid half angle results?
See attached images in my previous post
(sorry I understand my explanation of my issue is not too great)
Seem to be getting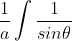
Ohh ok - Will make sure to remember that
Teacher told me its not a standard integral, so its best to use t-formula
If you dont mind, can you show me how I can finish off the solution from
Given t=tan(theta/2)
(just curious thats all)
Paradoxica
-insert title here-
Pretty sure you can just back-differentiate to obtain the answer.Solving the following integral:
I subbed x=tan(theta)
t=atan(theta/2)
Ohh ok - Will make sure to remember that
Teacher told me its not a standard integral, so its best to use t-formula
If you dont mind, can you show me how I can finish off the solution from)
Given t=tan(theta/2)
(just curious thats all)
Thankyou once again Integrand
You legend
Was wondering how I can stop leeching off the BOS community and give something back LOL
Probably not in the maths section, will look forward to helping out the physics and chemistry students tho
(after hscs
Paradoxica
-insert title here-
This will convert the integral into a standard form (look in your booklet bro)
The answer very rapidly comes out to be
Ohh ok - Will make sure to remember that
Teacher told me its not a standard integral, so its best to use t-formula
If you dont mind, can you show me how I can finish off the solution from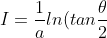 + C)
Given t=tan(theta/2)
(just curious thats all)
Paradoxica
-insert title here-
I personally think this situation is simply not necessary.
t-formulae are a path to disaster.
Paradoxica
-insert title here-
Refer to my previous post.T-formulae does allow the integral of cosec to come out nice and tidy, but there is no need for it at all
Also half the time a trig substitution is unnecessary for indefinite integrals.
But for definite integrals they are very slick.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
It's only tidy, if you have cosec by itself. (And it's still not necessary either, but it makes the final answer tidy)Refer to my previous post.
Also half the time a trig substitution is unnecessary for indefinite integrals.
But for definite integrals they are very slick.
