(
Another method)
The ball being pulled down 2cm from the origin implies that v = 0 at x = 2 or v(2) = 0. So we need an equation relating v and x.
Remember that
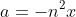
, which means
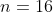
.
By chain rule,

Now, we have


Integrating both sides to arrive at

Use the initial condition (v = 0 at x = 2) to find that

So,

At extreme points,
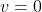
and solving for x gives
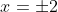
. So centre of motion is at
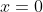
hence velocity at centre of motion is
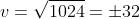
.