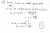Ok, not sure if solution is basically your method or not, they just moved everything in i) to one side assumed any point (x,y) with 2 solutions then showed product of roots was >1, next step was one of the roots had to be greater than 1. So angle had to be greater than pi/4 for 2 solutions... How did they go from if product of 2 roots (tan(theta)) is >1 that either root has to be >1? If you could explain this or give a simpler solution would be great - seems a lot of work for 1 mark!
View attachment 33365 <--- their solution