MATH1081 Discrete Maths (1 Viewer)

leehuan · Oct 16, 2016

Re: Discrete Maths Sem 2 2016

Given the vertex degrees, is there a rule of thumb that we can use to determine if there exists a simple graph with those degrees?

Drsoccerball · Oct 16, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
Given the vertex degrees, is there a rule of thumb that we can use to determine if there exists a simple graph with those degrees?

I think the way to go is to draw each vertex with its edges corresponding to its degree and look for any contradictions if you can draw it then no probs, if you can't then it doesn't exist ez.

leehuan · Oct 16, 2016

Re: Discrete Maths Sem 2 2016

Drsoccerball said:
I think the way to go is to draw each vertex with its edges corresponding to its degree and look for any contradictions if you can draw it then no probs, if you can't then it doesn't exist ez.

Yeah but like, I don't wanna run into experimental error lel

RealiseNothing · Oct 17, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
Given the vertex degrees, is there a rule of thumb that we can use to determine if there exists a simple graph with those degrees?

Not sure if this is what you mean, but say you know the vertex degrees are 2, 2, 2, 2, 3, 4, 4, then to test if such a graph exists then do this:

Write the degrees in ascending order:

2 2 2 2 3 4 4

Take the last number, get rid of it, and subtract 1 from the previous N numbers (where N is the last number).

In this case, get rid of the 4, then subtract 1 from the previous 4 numbers.

2 2 1 1 2 3

Re-order into ascending order:

1 1 2 2 2 3

Repeat:

1 1 1 1 1

You continue doing this until you either get a contradiction or a possible graph. In this case it is clear you can not graph this as the sum of the degrees is odd, contradiction.

leehuan · Oct 30, 2016

Re: Discrete Maths Sem 2 2016

Questions like these are what make me confused as to how to find the pigeons...

One thousand people have a pack of cards each. Every person chooses two cards from their pack. Prove that there must be at least 11 people who have chosen cards with exactly the same values (card rank)

leehuan · Oct 30, 2016

Re: Discrete Maths Sem 2 2016

$\text{Also is there a name for when }f\text{ and }f^{-1}\text{ are the same function?}\\ \text{e.g. }V = \{x\in \mathbb{N} \mid 1 \le x \le 10 \}, \quad f: V \to V$

$\text{where }f(x)\text{ is the inverse of }x\text{ modulo }11$

InteGrand · Oct 30, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
$\text{Also is there a name for when }f\text{ and }f^{-1}\text{ are the same function?}\\ \text{e.g. }V = \{x\in \mathbb{N} \mid 1 \le x \le 10 \}, \quad f: V \to V$

$\text{where }f(x)\text{ is the inverse of }x\text{ modulo }11$

Yeah, self-inverse functions are called involutions. You can read up about them and find examples of them here: https://en.wikipedia.org/wiki/Involution_(mathematics).

InteGrand · Oct 30, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
Questions like these are what make me confused as to how to find the pigeons...

One thousand people have a pack of cards each. Every person chooses two cards from their pack. Prove that there must be at least 11 people who have chosen cards with exactly the same values (card rank)

$\noindent The `holes' are pairs of values (like (Ace, King), (2, Jack), etc.), where the order of pairs doesn't matter. There are $13$ values to choose from for each entry in the unordered pair. The number of such pairs will be the $13$-th \textsl{triangular number}: $\frac{13\times 14}{2} = 13\times 7 = 91$. (Another way to get this is $\binom{13}{2} + 13$, since we could have either distinct values in the pair or same two values in the pair.) The `pigeons' are the $1000$ people. Note that $\Big{\lceil} \frac{1000}{91}\Big{\rceil} = 11$. So there exist at least $11$ people who have chosen exactly the same pair of values.$

leehuan · Oct 30, 2016

Re: Discrete Maths Sem 2 2016

InteGrand said:
$\noindent The `holes' are pairs of values (like (Ace, King), (2, Jack), etc.), where the order of pairs doesn't matter. There are $13$ values to choose from for each entry in the unordered pair. The number of such pairs will be the $13$-th \textsl{triangular number}: $\frac{13\times 14}{2} = 13\times 7 = 91$. (Another way to get this is $\binom{13}{2} + 13$, since we could have either distinct values in the pair or same two values in the pair.) The `pigeons' are the $1000$ people. Note that $\Big{\lceil} \frac{1000}{91}\Big{\rceil} = 11$. So there exist at least $11$ people who have chosen exactly the same pair of values.$

Didn't expect that the holes required that way of thought... I always seem to forget how to see things when it comes to PHP

leehuan · Oct 31, 2016

Re: Discrete Maths Sem 2 2016

Consider a set of 4 natural numbers

Can you use the pigeonhole principle to show that at least 2 are even or (inclusive or) at least 2 are odd?

(Or if not how would you do it without listing the cases)

InteGrand · Oct 31, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
Consider a set of 4 natural numbers

Can you use the pigeonhole principle to show that at least 2 are even or (inclusive or) at least 2 are odd?

(Or if not how would you do it without listing the cases)

The 'holes' would be the parity (odd or even) and the 'pigeons' the four numbers. There are two holes (odd or even). Since ceil(4/2) = 2, there are at least two numbers of the same parity.

leehuan · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

I just thought of this question on the spot and I don't imagine it to be too hard, but I want to see how someone would approach it.

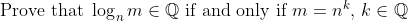
$\text{Prove that }\log_n m \in \mathbb{Q}\text{ if and only if }m=n^k,\, k \in \mathbb{Q}$

(Sincerely hope I didn't write something wrong here)

He-Mann · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

$\exists p,q \in \mathbb{Z}$ such that $ \mathrm{log}_nm = \frac{p}{q} \iff m = n^{p/q} = n^k $ where $k \in \mathbb{Q}. $ Conversely, suppose $m = n^k$, where $k \in \mathbb{Q}.$ Then take log base n on both sides gives, $\mathrm{log}_nm = k \in \mathbb{Q}.\quad \quad \quad \quad\square$

Drsoccerball · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

leehuan said:
I just thought of this question on the spot and I don't imagine it to be too hard, but I want to see how someone would approach it.

$\text{Prove that }\log_n m \in \mathbb{Q}\text{ if and only if }m=n^k,\, k \in \mathbb{Q}$

(Sincerely hope I didn't write something wrong here)

$$ Suppose $ \log_n m = \frac{a}{b} $ where a,b $ \in \mathbb{R}.$

$$ This implies that $ m^b = n^a$

$\therefore m = a^{\frac{a}{b}} = a^k $ as $ \frac{a}{b} \in \mathbb{Q}.$

$$ Consider the converse. $ m = n^k$

$Since k $ \in \mathbb{Q} $ that means it can be written as an integer over an integer$

$m = n^{\frac{c}{d}} $ and follow the same logic to get back to the logs. $ []$

He-Mann · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

New question

You have in front of you, a barrel of N ping pong balls, each labeled with a unique number. You pull a ball from the barrel, make a note of the label, and then put the ball back. After pulling K balls from the barrel, what is the probability that you've seen all of the balls? What happens when K=N and K>N. Consider these 2 cases separately.

Drsoccerball · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

He-Mann said:
New question

You have in front of you, a barrel of N ping pong balls, each labeled with a unique number. You pull a ball from the barrel, make a note of the label, and then put the ball back. After pulling K balls from the barrel, what is the probability that you've seen all of the balls? What happens when K=N and K>N. Consider these 2 cases separately.

n!/n^n ?

seanieg89 · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

The question can be rephrased as asking: "What is the probability of a randomly chosen f:X->Y being surjective if |X|=k and |Y|=n?"

The total number of functions between these sets is n^k.

The number of surjective functions arises from partitioning the |X| into n nonempty subsets and then constructing a bijection between these n subsets and the elements of Y.

The bijection part just gives you a factor of n!, the partitioning is the hard thing to count. The number of ways of partitioning an n-element set into k nonempty (unlabelled) subsets is S(n,k), called the Stirling numbers of the second kind.

So the answer is S(k,n)n!/n^k

It is obvious that S(n,n)=1, so that agrees with the answer provided above by drsoccerball for k=n.

S(k,n) does not have a nice closed form in general, but you can find summation expressions for it using inclusion-exclusion for example.

seanieg89 · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

Eg/

Let's compute the number of surjections from X to Y by inclusion exclusion. (This also computes S(k,n) by dividing out the n! factor.)

Let A be set of all functions from X to Y.

For each element y of Y, let A(y) be the set of all functions from X to Y that do not have y in their range.

Similarly, A(y1,y2) is defined to be the set of all functions from X to Y that do not have y1 or y2 in their range.

Etc.

Then inclusion-exclusion says that the number of functions in A that have range all of Y is given by:

$|A|-\sum_{y\in Y} |A(y)|+\sum_{y_1\neq y_2}|A(y_1,y_2)|-\ldots \\ \\ = n^k-n\cdot(n-1)^k+\binom{n}{2}\cdot (n-2)^k-\ldots\\ \\ = \sum_{j=0}^n (-1)^j\binom{n}{j}(n-j)^k\\ \\ = \sum_{j=0}^n (-1)^{n-j}\binom{n}{j}j^k\\ \\ \Rightarrow S(k,n)=\frac{1}{n!}\sum_{j=0}^n (-1)^{n-j}\binom{n}{j}j^k$

He-Mann · Nov 1, 2016

Re: Discrete Maths Sem 2 2016

seanieg89 said:
The question can be rephrased as asking: "What is the probability of a randomly chosen f:X->Y being surjective if |X|=k and |Y|=n?"

What is this 'heuristic' called? A reduction? An abstraction?

InteGrand · Nov 2, 2016

Re: Discrete Maths Sem 2 2016

He-Mann said:
What is this 'heuristic' called? A reduction? An abstraction?

I guess it's basically looking into the heart of the question. (It's phrased in terms of balls and boxes, but it's essentially a question about how many surjections we can make on given-sized (finite) domains and codomains.)

MATH1081 Discrete Maths (1 Viewer)

Well-Known Member

Well-Known Member

Well-Known Member

what is that?It is Cowpea

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Vexed?

Well-Known Member

Vexed?

Well-Known Member

Well-Known Member

Well-Known Member

Vexed?

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)