Hi All,
I'm currently stuck on a logarithmic question that i've been attempting for most of an hour with 0 success. There are no answers releases yet & any help would be appreciated
Question below
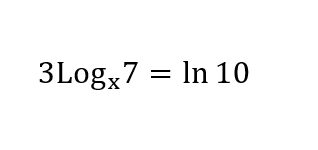
My main point of confusion comes to what rule to apply first. Do i first have to solve Ln(10) & then isolate the logarithmic function by dividing the answer by 3?
Note that i need to find the value "x"
I'm currently stuck on a logarithmic question that i've been attempting for most of an hour with 0 success. There are no answers releases yet & any help would be appreciated
Question below
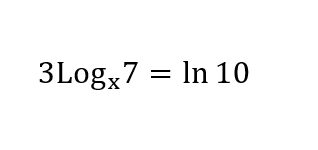
My main point of confusion comes to what rule to apply first. Do i first have to solve Ln(10) & then isolate the logarithmic function by dividing the answer by 3?
Note that i need to find the value "x"
Last edited:
