Approach 2: Dealing with the identity without getting bogged down in all the binomials - good approach or not?:
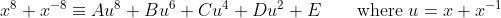
Firstly, it is obvious that the only term in the polynomial that can produce a term in
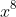
is
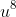
:
^8 \\ &= \binom{8}{0}x^8 + \binom{8}{1}x^7x^{-1} + \binom{8}{2}x^6x^{-2} + ... + \binom{8}{8}x^{-8} \\ &= x^8 + 8x^6 + 28x^4 + ... + x^{-8} \end{align*})
and the required term will be
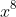
as
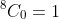
, so equating coefficients will give us that
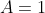
.
Second, we can get simultaneous equations by selective choice of values of

. Taking
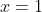
gives
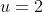
:
^8 + B(2)^6 + C(2)^4 + D(2)^2 + E \\ 1 + 1 &= 256 + 64B + 16C + 4D + E \\ 64B + 16C + 4D + E &= 2 - 256 \\ &= -254 \qquad \text{(1)} \end{align*})
For Extension 2 students,
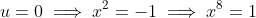
gives:
^8 + B(0)^6 + C(0)^4 + D(0)^2 + E \\ 2 &= E \end{align*})
This allows (1) to be simplified:
} \end{align*})
Now, consider
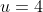
:
^2 &= x^2 + 2 + x^{-2} \\ 4^2 - 2 &= x^2 + x^{-2} \\ x^2 + x^{-2} &= 14 \\ \big(x^2 + x^{-2}\big)^2 &= 14^2 \\ x^4 + 2 + x^{-4} &= 14^2 = 196 \\ x^4 + x^{-4} &= 194 \\ \big(x^4 + x^{-4}\big)^2 &= 194^2 \\ x^8 + 2 + x^{-8} &= 194^2 = 37636 \\ x^8 + x^{-8} &= 37634 \\ \text{So,} \quad 37634 &= A(4)^8 + B(4)^6 + C(4)^4 + D(4)^2 + E \\ 37634 &= 65536 + 4096B + 256C + 16D + 2 \\ -1744 &= 256B +16C + D \\ -1680 &= 240B + 12C \qquad \text{on subtracting (1A)} \\ -140 &= 20B + C \qquad \text{(2)} \end{align*})
Recognising that further further substitutions will be equally messy, I would turn to the coefficient of
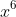
as it is obviously zero on the LHS of the identity and arises only fro the terms in
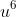
and
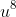
on RHS:
^6 \\ &= \binom{6}{0}x^6 + \binom{6}{1}x^5x^{-1} + \binom{6}{2}x^4x^{-2} + ... + \binom{6}{6}x^{-6} \\ &= x^6 + 6x^4 + 15x^2 + ... + x^{-6} \end{align*})
The term in
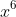
on the RHS is clearly
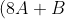x^6)
, giving us that
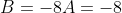
after equating coefficients. We can then use (2) to get that
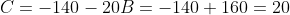
and then use (1A) to get that
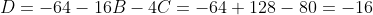
.
Thus, we have the results
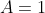
,
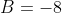
,
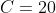
,
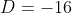
, and
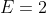
, as expected.
