-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Past Paper Mathematics 3U questions (1 Viewer)
- Thread starter frankfurt
- Start date
for q4, let the LHS = Rsin(theta + alpha). You will find 5sin(theta + tan^-1(4/3) = 5, so sin(theta + tan^-1(4/3) = 1. The new bounds are tan^-1(4/3) < x < 2pi + tan^-1(4/3). There is only one solution within these bounds (in the first quadrant).
Unknown Scholar
New Member
- Joined
- Oct 28, 2018
- Messages
- 22
- Gender
- Male
- HSC
- 2020
I could only do q10 with a brute force approach/ I'd never get this and there's probably a better way I can't think of right now.
So:
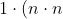, n\in\{2, 3, 4, 5, 6\} \Rightarrow 3\cdot 5=15) different permutations.
different permutations.
Now, let's consider all the square number that are available: 1, 4, 9, 25, 36, 64, 81, 100, 121, 144.
If we break down each square number into factors:
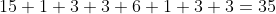
Total number of permutations:
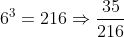
Since this is higher than all other options, then there must be a few we missed later with higher numbers.
Hence, D
So:
Now, let's consider all the square number that are available: 1, 4, 9, 25, 36, 64, 81, 100, 121, 144.
If we break down each square number into factors:
[+1]
[+3] - Three different ways to make this.
[+0] - We've already counted this.
[+3] - Three different ways for each different combination.
[+0] - We've already counted this.
[+6] - Three different ways for each different combination.
- Not possible
[+1]
- Not enough places to make anything.
[+3] - Three different ways to make this.
- Not possible
[+3] - Three different ways for each different combination.
Total number of permutations:
Since this is higher than all other options, then there must be a few we missed later with higher numbers.
Hence, D
Last edited:
right i see, thanks for helping me out!!for q4, let the LHS = Rsin(theta + alpha). You will find 5sin(theta + tan^-1(4/3) = 5, so sin(theta + tan^-1(4/3) = 1. The new bounds are tan^-1(4/3) < x < 2pi + tan^-1(4/3). There is only one solution within these bounds (in the first quadrant).
B1andB2
oui oui baguette
For Q4 you could also use the t-formula (I’m pretty sure it works) and so do the normal t- substitutions from the formula sheet, get a quadratic and you’ll end up with tan(theta/2)=1/2
solving for theta, you’ll end up finding that only one answer fits the domain.
solving for theta, you’ll end up finding that only one answer fits the domain.
- Joined
- Feb 16, 2005
- Messages
- 8,555
- Gender
- Male
- HSC
- 2006
For the second question, start with the scenario where the product of two values in the toss is already a perfect square. This should cover the majority of the cases.
When the product of the two values is already a perfect square, then the only way to get the final product to be a perfect square is for the third value to also be perfect square (i.e. 1 or 4). This means matching the pairs (1x1), (2x2), (3x3), (4x4), (5x5) and (6x6) with 1 or 4.
When 1 is matched with (1x1) there is only 1 way of doing this, but for the other pairs there are 3 ways of doing this, so there 1+3x5 arrangements. Similarly apply that to matching the 4 and you get a total of 2x(1+3x5) arrangements.
However, note that since 4 and 6 are not prime numbers you can find other ways to generate the perfect square by breaking them down into their prime factors. Turns out we've counted most of them already, except for 6=2x3. There are 6 ways to arrange the (2,3,6) so add that to your answer and you get 38 possibilities.
When the product of the two values is already a perfect square, then the only way to get the final product to be a perfect square is for the third value to also be perfect square (i.e. 1 or 4). This means matching the pairs (1x1), (2x2), (3x3), (4x4), (5x5) and (6x6) with 1 or 4.
When 1 is matched with (1x1) there is only 1 way of doing this, but for the other pairs there are 3 ways of doing this, so there 1+3x5 arrangements. Similarly apply that to matching the 4 and you get a total of 2x(1+3x5) arrangements.
However, note that since 4 and 6 are not prime numbers you can find other ways to generate the perfect square by breaking them down into their prime factors. Turns out we've counted most of them already, except for 6=2x3. There are 6 ways to arrange the (2,3,6) so add that to your answer and you get 38 possibilities.
thanks!I could only do q10 with a brute force approach/ I'd never get this and there's probably a better way I can't think of right now.
So:
different permutations.
Now, let's consider all the square number that are available: 1, 4, 9, 25, 36, 64, 81, 100, 121, 144.
If we break down each square number into factors:
Total:
[+1]
[+3] - Three different ways to make this.
[+0] - We've already counted this.
[+3] - Three different ways for each different combination.
[+0] - We've already counted this.
[+6] - Three different ways for each different combination.
- Not possible
[+1]
- Not enough places to make anything.
[+3] - Three different ways to make this.
- Not possible
[+3] - Three different ways for each different combination.
Total number of permutations:
Since this is higher than all other options, then there must be a few we missed later with higher numbers.
Hence, D
The second question, about the product of the value on three dice being a perfect square, I think comes from the Independent Schools paper, with the options given in the source as:
 } \ \ \ \ &\frac{10}{216} \\ \\ \text{(B) } \ \ \ \ &\frac{22}{216} \\ \\ \text{(C) } \ \ \ \ &\frac{25}{216} \\ \\ \text{(D) } \ \ \ \ &\frac{31}{216} \end{align*})
I am aware of at least one other school that used the question with this set of choices, which I note do not include the correct answer. I have found one school (possibly the source of the OP's question as the four options offered are the same) that changed the selection to include the correct answer... but didn't keep the original answer as a distractor.
Definitely an embarrassing error for whoever wrote the original!
I am aware of at least one other school that used the question with this set of choices, which I note do not include the correct answer. I have found one school (possibly the source of the OP's question as the four options offered are the same) that changed the selection to include the correct answer... but didn't keep the original answer as a distractor.
Definitely an embarrassing error for whoever wrote the original!



