Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Permutation and combinations, confusing question (1 Viewer)
- Thread starter Haz_taz
- Start date
The problem can be rewritten as:How many ways can you make change for 50 cents using 5, 10 and 20 cent pieces
(10,0,0)
(8,1,0)
(6,2,0)
(6,0,1)
(4,3,0)
(4,1,1)
(2,0,2)
(2,4,0)
(2,2,1)
(0,5,0)
(0,1,2)
(0,3,1)
Notice how the 5 cents must always be even as
Last edited:
Thanks for the answer, i think i understand how to solve this but the book says answer is 12The problem can be rewritten as:
or
where x= no of 5c coins, y=no of 10c coins z=no of 20c coins. From here we could just list out the possibilities of of the triplet (x,y,z) given that x,y,z are non-negative integers. So:
(10,0,0)
(8,1,0)
(6,2,0)
(6,0,1)
(4,3,0)
(4,1,1)
(2,0,2)
(2,4,0)
(0,5,0)
(0,1,2)
(0,3,1)
Notice how the 5 cents must always be even as.
Ahh I missed (2,2,1)Thanks for the answer, i think i understand how to solve this but the book says answer is 12
THANKS ALOT FOR THE HELP I WAS STUCK ON THIS QUESTIONS OMG!!Ahh I missed (2,2,1)
Now our second way of solving the equation 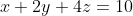 is to rewrite it as
is to rewrite it as 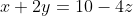 . y can vary such that
. y can vary such that 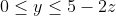 and the RHS must obv be non-negative and an integer so
and the RHS must obv be non-negative and an integer so 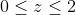 . Now we could use the 'stars and bars method,' but Ill go for a more intuitive approach. Let
. Now we could use the 'stars and bars method,' but Ill go for a more intuitive approach. Let 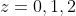 this means:
this means: 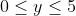 ,
, 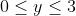 ,
, 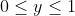 respectively. So the possible values of y for each case are:
respectively. So the possible values of y for each case are: ) ,
, ) ,
, ) in total=12.
in total=12.
Perms and Combs are the necessary evil of the HSC Maths syllabi.. that one question from the 2020 Extension 1 HSC paper still makes me shudder at the sight of itDamn y'all out here doing perms and combs I've already given up on em hahahah
Bruh perms and combs should just be taken out of the syllabus, I suffered a good 2 weeks of pain covering it in schoolPerms and Combs are the necessary evil of the HSC Maths syllabi.. that one question from the 2020 Extension 1 HSC paper still makes me shudder at the sight of it
It won't be any time soon if NESA decide take out Perms and Combs and make English an optional subject in the HSC. You gotta do what you gotta do thoughBruh perms and combs should just be taken out of the syllabus, I suffered a good 2 weeks of pain covering it in school
The chances that NESA would take P&C out and make English optional would both be equally slim in terms of probability, I mean it's already confirmed NESA hates everyone -_-It won't be any time soon if NESA decide take out Perms and Combs and make English an optional subject in the HSC. You gotta do what you gotta do though
Well I suppose that alleviates half of the pain I'll have during my MX2 HSC examDon't complain too much lol. Permutations and combinations used to appear in Maths Ext2 papers until the new syllabus came in.
Perms and combs are my fav. Whats wrong with you kids. Just get more brainpower lol.
Y tf do u know stars and bars. Is that in syllabus?Now our second way of solving the equationis to rewrite it as
. y can vary such that
and the RHS must obv be non-negative and an integer so
. Now we could use the 'stars and bars method,' but Ill go for a more intuitive approach. Let
this means:
,
,
respectively. So the possible values of y for each case are:
,
,
in total=12.
Last edited:
Harder mx1 in mx2 was maybe the hardest mx2 topic lol.Well I suppose that alleviates half of the pain I'll have during my MX2 HSC exam
Wdym stars and barring. I don't see how or why you would stars and bars. Show me the stars and barring way?Now our second way of solving the equationis to rewrite it as
. y can vary such that
and the RHS must obv be non-negative and an integer so
. Now we could use the 'stars and bars method,' but Ill go for a more intuitive approach. Let
this means:
,
,
respectively. So the possible values of y for each case are:
,
,
in total=12.
I call cap on @Qeru stars and barring.Wdym stars and barring. I don't see how or why you would stars and bars. Show me the stars and barring way?
Let there beWdym stars and barring. I don't see how or why you would stars and bars. Show me the stars and barring way?
When I was first taught “stars and bars” (in year 8 or 9 I think) it was called it the “supermarket principle” using the analogy of trying to arrange different fruits and vegetables at a supermarket checkout using plastic dividers  . I have never seen it cited as such since.
. I have never seen it cited as such since.
smart.Let there bestars and 1 bar (since we want to split 5-2z into two parts the number of stars in each part is x and y). We can arrange these in
ways (including the extra bar we have 6-2z objects needed to be arranged). Now all we have to do is sum this up from z=0-2 so
.

