We have a function
)
where
=N_0)
, a constant, which satisfies the differential equation (DE)
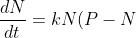 \qquad \text{. . . . . . . . (*)})
where

and
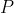
are constants.
(a) Let
)
be a function related to
)
by the equation
 = P \times y(t))
. It follows that
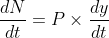
which can be substituted into (*) to give:
 \\ P\frac{dy}{dt}&=kPy(P-Py) \\ &=kP^2y(1-y) \\ \frac{dy}{dt}&=kPy(1-y) \end{align*})
Now, let
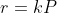
, a constant, and the DE becomes:
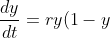 \qquad \text{. . . . . . . . (**)})
with the initial value of
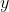
being
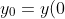 = \frac{N(0)}{P} = \frac{N_0}{P})
.
(b) Let

be a variable related to time by
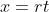
, from which it follows that
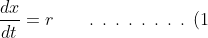})
.
From the Chain Rule, we know that
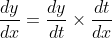
and we can substitute (**) and (1) into this to get
\times\frac{1}{r} \\ &=y(1-y) \qquad \text{. . . . . . . . (***)} \end{align*})
which is a DE in two variables,

and
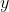
. At
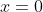
, it has the initial value
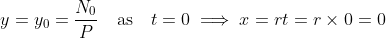
.
(c) Let

be a variable related to
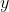
by
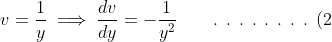)
from which it follows that
 \quad \text{using (2) and (***)} \\ &= \frac{y - 1}{y} \\ &= 1 - \frac{1}{y} \\ &=1-v \end{align*})
The problem has now been transformed into one that can be solved by integration without the need to use partial fractions:
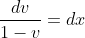
I'll leave the rest for you to work on.


