anyone know where to find good q's for 2nd order recursion proofs, Cambridge only has a handful of basic ones, not sure where to find anymore. Also i dont want to look through past papers as i would like to keep them for trial period. thanks.
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2nd order recursion (1 Viewer)
- Thread starter tito981
- Start date
isnt recursion 3u?anyone know where to find good q's for 2nd order recursion proofs, Cambridge only has a handful of basic ones, not sure where to find anymore. Also i dont want to look through past papers as i would like to keep them for trial period. thanks.
Ice-Cream-Man
Member
- Joined
- May 25, 2020
- Messages
- 31
- Gender
- Undisclosed
- HSC
- N/A
thought so as well
isnt recursion 3u?
thought so as well
nah, not 2nd order recursive ones.isnt recursion 3u?
are these in chapter 2?nah, not 2nd order recursive ones.
yeare these in chapter 2?
where
enrichment 2E, q22where
both ive seen the Un realtionships but i can only find first order ones. I would also like more challenging recursion material if possible.Are you after examples of proving the formula forgiven a recursion relationship and initial conditions, or more challenging material that uses second order recursions?
A few questions to ponder...
The Fibonacci Sequence is defined as follows:
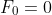
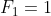
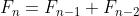 for all integers
for all integers 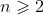
One formula for the general formula for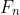 is called Binet's formula, which states that, for all non-negative integers
is called Binet's formula, which states that, for all non-negative integers  :
:
^n - \frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n)
Question 1
(a) Prove by induction that
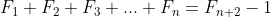 .
.
(b) Prove, without using induction, that
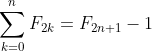 .
.
(c) Hence, simplify
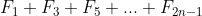 .
.
Question 2
(a) List the values of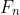 for
for 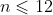 and note the pattern of the even terms in the sequence. State a theorem related to generalise this pattern and prove it without using induction.
and note the pattern of the even terms in the sequence. State a theorem related to generalise this pattern and prove it without using induction.
(b) Use induction to show that all terms of the form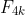 are divisible by 3.
are divisible by 3.
(c) Prove that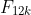 is a multiple of 12. You may use the fact that
is a multiple of 12. You may use the fact that 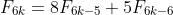 .
.
Question 3
(a) Show that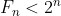 for all
for all 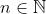 .
.
(b) Find the smallest integer such that
such that 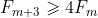 .
.
(c) Hence, prove that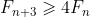 for all integers
for all integers 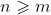
Question 4
(a) Using induction, prove that, if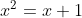 then
then 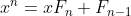 for all integers
for all integers 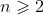 .
.
(b) Using the result in part (a), derive Binet's formula.
(c) Use strong induction to provide a different proof of Binet's formula, that
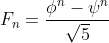
where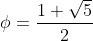 and
and 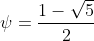 .Note that
.Note that 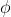 is often called the "golden ratio."
is often called the "golden ratio."
(d) Show that
^n}{\sqrt{5}} = \frac{\phi^n-(-\phi)^{-n}}{\sqrt{5}}) and hence show that
and hence show that 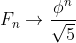 as
as 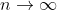 .
.
(e) Use Binet's formula to prove that
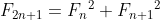 and hence, or otherwise, show that
and hence, or otherwise, show that
)
Question 5
Let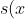 = \sum_{k=0}^\infty F_k x^k)
(a) Show that
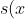 = \frac{x}{1-x-x^2}) .Note: This result is only true if
.Note: This result is only true if 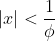 .
.
(b) Explain why the result is invalid for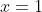 and
and 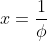 .
.
(c) Find the value of
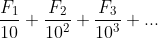
Question 6
The Lucas Numbers are a set of numbers that are closely related to the Fibonacci sequence. They are defined by:
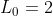
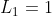
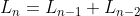 for all integers
for all integers 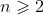
(a) Prove that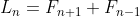 for all
for all 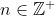
(b) Prove that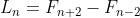 for all integers
for all integers 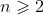
(c) A general formula used for calculating large Fibonacci numbers is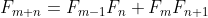 .
.
(c)(i) Prove this result by induction on by taking
by taking  as a constant.
as a constant.
(c)(ii) A result given in question 2(c) was that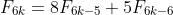 . Show that this is a special case of the general formula.
. Show that this is a special case of the general formula.
(c)(iii) Show that the results in 4(e) are also special cases of this formula.
(d) Use the formula in part (c) to prove that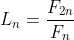 .
.
(e) Using Binet's formula, derive a general formula for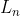 .
.
(f) Show that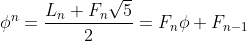 and hence prove that
and hence prove that 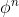 is irrational for all
is irrational for all 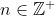 .
.
The Fibonacci Sequence is defined as follows:
One formula for the general formula for
Question 1
(a) Prove by induction that
(b) Prove, without using induction, that
(c) Hence, simplify
Question 2
(a) List the values of
(b) Use induction to show that all terms of the form
(c) Prove that
Question 3
(a) Show that
(b) Find the smallest integer
(c) Hence, prove that
Question 4
(a) Using induction, prove that, if
(b) Using the result in part (a), derive Binet's formula.
(c) Use strong induction to provide a different proof of Binet's formula, that
where
(d) Show that
(e) Use Binet's formula to prove that
Question 5
Let
(a) Show that
(b) Explain why the result is invalid for
(c) Find the value of
Question 6
The Lucas Numbers are a set of numbers that are closely related to the Fibonacci sequence. They are defined by:
(a) Prove that
(b) Prove that
(c) A general formula used for calculating large Fibonacci numbers is
(c)(i) Prove this result by induction on
(c)(ii) A result given in question 2(c) was that
(c)(iii) Show that the results in 4(e) are also special cases of this formula.
(d) Use the formula in part (c) to prove that
(e) Using Binet's formula, derive a general formula for
(f) Show that
Last edited:
Question 7
In question 2(a), you found that the the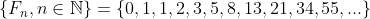 , and thus established that
, and thus established that 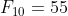 .
.
In question 4(e), the formulae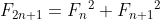 and
and ) were established.
were established.
(a) Using only the values in the Fibonacci sequence shown above and the formulae from question 4(e), establish that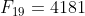 .
.
(b) Using Binet's formula and the binomial theorem, and without using a calculator, establish the value of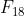 . Check your answer using one of the above formulae and comment on the relative difficulty in these approaches for determining the values of members of the Fibonacci sequence without determining them sequentially from the recurrence relation.
. Check your answer using one of the above formulae and comment on the relative difficulty in these approaches for determining the values of members of the Fibonacci sequence without determining them sequentially from the recurrence relation.
(c) Earlier members of the sequence can be calculated from later values if those are known. Show that
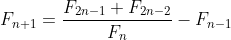
and use this result to confirm that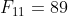 .
.
(d) Find the value of and use your result to find the value of
and use your result to find the value of 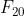 . Check your results using the recurrence relation and your results from (a) and (b).
. Check your results using the recurrence relation and your results from (a) and (b).
(e) Show that the prime factorisation of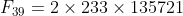 and find the prime factorisation of
and find the prime factorisation of 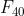 .
.
(f) Determine the percentage error in the estimate
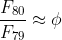
(g) In question 6(c), a general calculating formula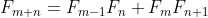 was proved. Use it to show that, in scientific notation,
was proved. Use it to show that, in scientific notation,
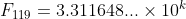
and determine the value of the integer .
.
In question 2(a), you found that the the
In question 4(e), the formulae
(a) Using only the values in the Fibonacci sequence shown above and the formulae from question 4(e), establish that
(b) Using Binet's formula and the binomial theorem, and without using a calculator, establish the value of
(c) Earlier members of the sequence can be calculated from later values if those are known. Show that
and use this result to confirm that
(d) Find the value of
(e) Show that the prime factorisation of
(f) Determine the percentage error in the estimate
(g) In question 6(c), a general calculating formula
and determine the value of the integer
u might as well just write and publish a question book lol.Question 7
In question 2(a), you found that the the, and thus established that
.
In question 4(e), the formulaeand
were established.
(a) Using only the values in the Fibonacci sequence shown above and the formulae from question 4(e), establish that.
(b) Using Binet's formula and the binomial theorem, and without using a calculator, establish the value of. Check your answer using one of the above formulae and comment on the relative difficulty in these approaches for determining the values of members of the Fibonacci sequence without determining them sequentially from the recurrence relation.
(c) Earlier members of the sequence can be calculated from later values if those are known. Show that
and use this result to confirm that.
(d) Find the value ofand use your result to find the value of
. Check your results using the recurrence relation and your results from (a) and (b).
(e) Show that the prime factorisation ofand find the prime factorisation of
.
(f) Determine the percentage error in the estimate
(g) In question 6(c), a general calculating formulawas proved. Use it to show that, in scientific notation,
and determine the value of the integer.
Since I have no life Ill attempt these (some working may be left out due to sheer number of questions):A few questions to ponder...
The Fibonacci Sequence is defined as follows:
for all integers
One formula for the general formula foris called Binet's formula, which states that, for all non-negative integers
:
Question 1
(a) Prove by induction that
.
(b) Prove, without using induction, that
.
(c) Hence, simplify
.
Question 2
(a) List the values offor
and note the pattern of the even terms in the sequence. State a theorem related to generalise this pattern and prove it without using induction.
(b) Use induction to show that all terms of the formare divisible by 3.
(c) Prove thatis a multiple of 12. You may use the fact that
.
Question 3
(a) Show thatfor all
.
(b) Find the smallest integersuch that
.
(c) Hence, prove thatfor all integers
Question 4
(a) Using induction, prove that, ifthen
for all integers
.
(b) Using the result in part (a), derive Binet's formula.
(c) Use strong induction to provide a different proof of Binet's formula, that
Note that
whereand
.
is often called the "golden ratio."
(d) Show that
and hence show that
as
.
(e) Use Binet's formula to prove that
and hence, or otherwise, show that
Question 5
Let
(a) Show that
Note: This result is only true if.
.
(b) Explain why the result is invalid forand
.
(c) Find the value of
Question 6
The Lucas Numbers are a set of numbers that are closely related to the Fibonacci sequence. They are defined by:
for all integers
(a) Prove thatfor all
(b) Prove thatfor all integers
(c) A general formula used for calculating large Fibonacci numbers is.
(c)(i) Prove this result by induction onby taking
as a constant.
(c)(ii) A result given in question 2(c) was that. Show that this is a special case of the general formula.
(c)(iii) Show that the results in 4(e) are also special cases of this formula.
(d) Use the formula in part (c) to prove that.
(e) Using Binet's formula, derive a general formula for.
(f) Show thatand hence prove that
is irrational for all
.
1.
(a) n=1 is easy to see. Assume:
(b)The idea is to repeatedly use the definition of the fibonacci sequence on the RHS so:
.
.
.
(c) Replace n with 2n in the result in (a) then subtract the result in (b) to get:
2. (a) 0,1,1,2,3,5,8,13,21,34,55,89,144, even terms are 0,1,3,8,21,55,144... Notice how 3=(2x1)+1. 8=(2x3+1)+1, 21=(2x8+3+1)+1, 55=(2x21+8+3+1)+1 and so on. Therefore a pattern is:
(b) k=0 is trivally true. Assume for k=r i.e.
(c) We use a similar method to (b) knowing that
3.
(a) Trivial for n=0 and n=1 and n=2 (if you dont count 0 as a natural number). Assume for n=k and n=k+1:
(b) We can just guess and check this by first writing out a few fibonacci numbers: 0,1,1,2,3,5,8,13 and conclude that m=2 since 5>1x4.
(c) m=2 proven in b. m=3 is also easy to verify . Assume for n=k and n=k+1
4.
(a) base case trivial, assume n=k:
(b) Solving the initial quadratic gives solutions:
Subtracting the equations gives:
So:
(c) n=0,1 basic algebra. Assume true for n=k and n=k+1 and adding:
But we know
(d)
As
(e)
To prove the second identity we use the prev identity:
and: Replacing n with n-1 gives:
Now using the definition of the fibonacci sequence in eqn 1:
subbing in eqn 2:
The rest coming soon......
Nice job! You should attend the BOS trials this year because you seem to really like Maths.Since I have no life Ill attempt these (some working may be left out due to sheer number of questions):
1.
(a) n=1 is easy to see. Assume:. Add
to both sides:
, now use the definition of the fibonacci sequence to get:
, therefore true for n=k+1.
(b)The idea is to repeatedly use the definition of the fibonacci sequence on the RHS so:
.
.
.
(c) Replace n with 2n in the result in (a) then subtract the result in (b) to get:
2. (a) 0,1,1,2,3,5,8,13,21,34,55,89,144, even terms are 0,1,3,8,21,55,144... Notice how 3=(2x1)+1. 8=(2x3+1)+1, 21=(2x8+3+1)+1, 55=(2x21+8+3+1)+1 and so on. Therefore a pattern is:. To prove this we use the result in 1(b) replacing n with n-2 to get:
(b) k=0 is trivally true. Assume for k=r i.e.where B is an integer. For k=r+1:
assumption and know that F_4=3
(c) We use a similar method to (b) knowing thatthe identity could also be used to compute f_12 faster.
3.
(a) Trivial for n=0 and n=1 and n=2 (if you dont count 0 as a natural number). Assume for n=k and n=k+1:and
and these two to get:
(b) We can just guess and check this by first writing out a few fibonacci numbers: 0,1,1,2,3,5,8,13 and conclude that m=2 since 5>1x4.
(c) m=2 proven in b. m=3 is also easy to verify . Assume for n=k and n=k+1and
Adding these two:
4.
(a) base case trivial, assume n=k:prove n=k+1,
Fibonacci definition
using the given identity.
assumption
(b) Solving the initial quadratic gives solutions:and
let these be
and
respectively. Therefore we have the simultaneous equations:
Subtracting the equations gives:
So:
(c) n=0,1 basic algebra. Assume true for n=k and n=k+1 and adding:
But we knowand
since these two constants satisfy the equation:
(d)also:
.
As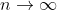
since
therefore:
(e)
By product of roots:
it was proven eariler that
To prove the second identity we use the prev identity:
and: Replacing n with n-1 gives:
Now using the definition of the fibonacci sequence in eqn 1:
subbing in eqn 2:
The rest coming soon......
We will see hahaNice job! You should attend the BOS trials this year because you seem to really like Maths.
he's too scared of me to attend.Nice job! You should attend the BOS trials this year because you seem to really like Maths.
We will see haha
Are you aiming for over a 99.95?Since I have no life Ill attempt these (some working may be left out due to sheer number of questions):
1.
(a) n=1 is easy to see. Assume:. Add
to both sides:
, now use the definition of the fibonacci sequence to get:
, therefore true for n=k+1.
(b)The idea is to repeatedly use the definition of the fibonacci sequence on the RHS so:
.
.
.
(c) Replace n with 2n in the result in (a) then subtract the result in (b) to get:
2. (a) 0,1,1,2,3,5,8,13,21,34,55,89,144, even terms are 0,1,3,8,21,55,144... Notice how 3=(2x1)+1. 8=(2x3+1)+1, 21=(2x8+3+1)+1, 55=(2x21+8+3+1)+1 and so on. Therefore a pattern is:. To prove this we use the result in 1(b) replacing n with n-2 to get:
(b) k=0 is trivally true. Assume for k=r i.e.where B is an integer. For k=r+1:
assumption and know that F_4=3
(c) We use a similar method to (b) knowing thatthe identity could also be used to compute f_12 faster.
3.
(a) Trivial for n=0 and n=1 and n=2 (if you dont count 0 as a natural number). Assume for n=k and n=k+1:and
and these two to get:
(b) We can just guess and check this by first writing out a few fibonacci numbers: 0,1,1,2,3,5,8,13 and conclude that m=2 since 5>1x4.
(c) m=2 proven in b. m=3 is also easy to verify . Assume for n=k and n=k+1and
Adding these two:
4.
(a) base case trivial, assume n=k:prove n=k+1,
Fibonacci definition
using the given identity.
assumption
(b) Solving the initial quadratic gives solutions:and
let these be
and
respectively. Therefore we have the simultaneous equations:
Subtracting the equations gives:
So:
(c) n=0,1 basic algebra. Assume true for n=k and n=k+1 and adding:
But we knowand
since these two constants satisfy the equation:
(d)also:
.
As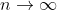
since
therefore:
(e)
By product of roots:
it was proven eariler that
To prove the second identity we use the prev identity:
and: Replacing n with n-1 gives:
Now using the definition of the fibonacci sequence in eqn 1:
subbing in eqn 2:
The rest coming soon......
Despite what I've heard about the BOS trials being challenging I think this guy gonna ace it, better put some hard as hell q for him if he decides to participateNice job! You should attend the BOS trials this year because you seem to really like Maths.
Trust me every question I've answered on this site is nothing compared to BOS.Despite what I've heard about the BOS trials being challenging I think this guy gonna ace it, better put some hard as hell q for him if he decides to participate
