OreoMcFlurry
Member
- Joined
- Jul 13, 2021
- Messages
- 40
- Gender
- Male
- HSC
- 2021
I was practicing mod 5 (advanced mechanics), and I stumbled across this question:

I put A - as it's just logical to think that as per Kepler's second law, an orbiting object covers the same area of space in the same amount of time no matter where it is in its orbit.

Hence, if an object is in it's aphelion or apogee (furthest point of orbit away from the central body) - then: Ep>Ek (energy is conserved)
and likewise, if an object is in it's perihelion or perigee (closest point of orbit from the central body) - then: Ek>Ep (energy is conserved)
It would be then logical to think that if an orbiting object were to cover a particular distance (arc length of orbit), the object at the perihelion would cover that fixed arc length in less time than the same object at the apohelion.
To prove that A is the answer, I used some HSC Maths Extension 1 techniques. If any of you are interested, I've attached it:
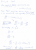
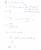

I put A - as it's just logical to think that as per Kepler's second law, an orbiting object covers the same area of space in the same amount of time no matter where it is in its orbit.

Hence, if an object is in it's aphelion or apogee (furthest point of orbit away from the central body) - then: Ep>Ek (energy is conserved)
and likewise, if an object is in it's perihelion or perigee (closest point of orbit from the central body) - then: Ek>Ep (energy is conserved)
It would be then logical to think that if an orbiting object were to cover a particular distance (arc length of orbit), the object at the perihelion would cover that fixed arc length in less time than the same object at the apohelion.
To prove that A is the answer, I used some HSC Maths Extension 1 techniques. If any of you are interested, I've attached it:
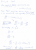
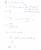
Attachments
-
2 KB Views: 3
-
205.2 KB Views: 3