-
Looking for HSC notes and resources? Check out our Notes & Resources page
[Complex Numbers] Ex 1E Q22) | [Solved] (1 Viewer)
- Thread starter A1La5
- Start date
https://boredofstudies.org/threads/harder-complex-number-question.181881/
Exact same question was answered here.
@A1La5, })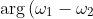
is not the exterior angle of the triangle that you have drawn. Leaving aside that this argument is negative and the angle that you are calling the exterior angle is positive, the exterior angle of a triangle at a vertex must be between one of the sides that meet at that vertex and the other side the meets at that vertex produced.
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
})
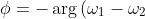(as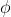 
is a positive angle in a triangle but 
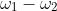has a negative argument),
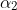, and the third angle in the triangle that you have not named. Let's call it 
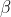, so that your triangle has angles 
, 
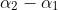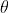, and 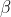(though you don't actually need ).
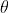You first need to find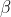, so that a second application of co-interior angles with 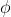, , 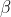and 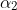allows you to find .
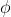As you have recognised that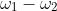 is a vector from 
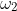to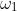 
, you need only complete the parallelogram with 
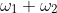as the second diagonal (i.e., with vertices at 
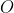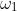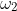, , , and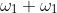 
).
Note that the interior angles of this parallelogram are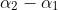 and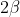 
, and these angles are supplementary, which gives you that
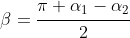
and from that you can find the size of
 - 2\alpha_2}{2} = \cfrac{\pi - \alpha_1 - \alpha_2}{2})
and hence you can determine the principal argument of.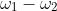
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
You first need to find
As you have recognised that
Note that the interior angles of this parallelogram are
and from that you can find the size of
and hence you can determine the principal argument of
It's worth noting that the thread that @Drdusk points to takes a different approach, finding my angle 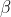without completing the parallelogram by instead using the given fact that 
. This makes the triangle that @A1La5 drew above an isosceles triangle, from which it follows that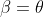 
as these are its base angles. Both approaches are valid, of course.
Damm, looks like I was a lot further from the solution then I thought. Thanks so much for your help!@A1La5,
The theorem you need is that co-interior angles on parallel lines are supplementary, with the angles being
You first need to find
As you have recognised that
Note that the interior angles of this parallelogram are
and from that you can find the size of
and hence you can determine the principal argument of
EDIT: @CM_Tutor, would the horizontal line drawn from
Last edited:
Yes, absolutely. It is the fact that it is parallel to theEDIT: @CM_Tutor, would the horizontal line drawn from
from which you can find
I am not seeing what pair of parallel lines you mean. In your second diagram, it looks like the angle you have labelled asIf so, then can we also use alternate angles + the angle sum of a triangle (with angles
However, if you were to produce the side of the triangle that is represented by
This would be an alternative way to establish that
Yeah, guess I should've clarified. The two parallel lines that I'm talking about would be the horizontal line drawn from
In this diagram I have marked the two parallel sides I am referring to.
First, I used the fact that the triangle in the original diagram is isosceles (as both
Now, I redrew a triangle from this above diagram below.
The side opposite
After this the result just falls out, using your definition of
Last edited:
