If you think through what is described, we have
- Snow fall in week 1 = 5 cm
- Snow fall in week 2 = 5 + 2 = 7 cm
- Snow fall in week 3 = 7 + 2 = 9 cm
- Snow fall in week 4 = 9 + 2 = 11 cm
- ... pattern continues ...
- Snow fall in week 9 = 19 + 2 = 21 cm
- Snow fall in week 10 = 21 + 2 = 23 cm
- Snow fall in week 11 = 23 + 2 = 25 cm
We are told that the pattern changes at the middle week of the season from increasing snow fall to decreasing snow fall.
In a 21 week season, week 11 is the middle week as there are 10 weeks before it and 10 weeks after it. So, we then get...
- Snow fall in week 12 = 25 - 2 = 23 cm
- Snow fall in week 13 = 23 - 2 = 21 cm
- Snow fall in week 14 = 21 - 2 = 19 cm
- ... pattern continues ...
- Snow fall in week 19 = 11 - 2 = 9 cm
- Snow fall in week 20 = 9 - 2 = 7 cm
- Snow fall in week 21 = 7 - 2 = 5 cm
Our total snow fall over the season is then
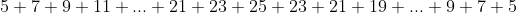
This entire series is NOT an AP as there it is not a constant common difference. So, we need to manipulate it to make one or more series that can be found using AP formulae. This can be done in a number of ways, and whichever you adopt will lead to the correct answer... though the last one is the most efficient:
Approach 1(a): Divide the series where the common difference changes

 + \bigg(23 + 21 + 19 + ... + 9 + 7 + 5\bigg))
Each set of brackets contains an AP:
- First bracket
 is an AP of 11 terms (weeks 1 to 11, inclusive) which has
is an AP of 11 terms (weeks 1 to 11, inclusive) which has 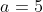 ,
,  , and
, and  .
.
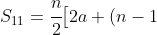d\big] = \cfrac{11}{2}\big[2 \times 5 + (11-1) \times 2\big] = \cfrac{11}{2} \times 30 = 165)
- Second bracket
 is an AP of 10 terms (weeks 12 to 21, inclusive) which has
is an AP of 10 terms (weeks 12 to 21, inclusive) which has  ,
,  , and
, and  .
.
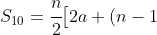d\big] = \cfrac{10}{2}\big[2 \times 23 + (10-1) \times -2\big] = 5 \times 28 = 140)
 + \bigg(23 + 21 + 19 + ... + 9 + 7 + 5\bigg) \\ &= S_{11} + S_{10} \\ &= 165 + 140 \\ &= 305\ \text{cm} \end{align*})

 + \bigg(25 + 23 + 21 + ... + 9 + 7 + 5\bigg))
Each set of brackets contains an AP:
- First bracket
 is an AP of 10 terms (weeks 1 to 10, inclusive) which has
is an AP of 10 terms (weeks 1 to 10, inclusive) which has 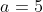 ,
,  , and
, and  .
.
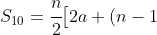d\big] = \cfrac{10}{2}\big[2 \times 5 + (10-1) \times 2\big] = 5 \times 28 = 140)
- Second bracket
 is an AP of 11 terms (weeks 11 to 21, inclusive) which has
is an AP of 11 terms (weeks 11 to 21, inclusive) which has  ,
,  , and
, and  .
.
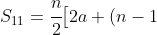d\big] = \cfrac{11}{2}\big[2 \times 25 + (11-1) \times -2\big] = \cfrac{11}{2} \times 30 = 165)
 + \bigg(25 + 23 + 21 + ... + 9 + 7 + 5\bigg) \\ &= S_{10} + S_{11} \\ &= 140 + 165 \\ &= 305\ \text{cm} \end{align*})
 + 25 + \bigg(23 + 21 + ... + 9 + 7 + 5\bigg) \\ &= 2\bigg(5 + 7 + 9 + 11 + ... + 21 + 23\bigg) + 25 \end{align*})
This rearrangement works by recognising that the increasing pattern of weeks 1 to 10 is also the pattern for weeks 12 to 21, but in reverse. Thus, we have that
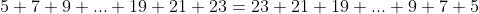
. We now have only one set of brackets and a single AP, plus an extra term that needs to be added:
 is an AP of 10 terms (weeks 1 to 10, forwards, which is the same as weeks 12 to 21, backwards - inclusive in each case) which has
is an AP of 10 terms (weeks 1 to 10, forwards, which is the same as weeks 12 to 21, backwards - inclusive in each case) which has 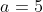 ,
,  , and
, and  .
.
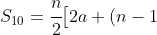d\big] = \cfrac{10}{2}\big[2 \times 5 + (10-1) \times 2\big] = 5 \times 28 = 140)
 + 25 + \bigg(23 + 21 + ... + 9 + 7 + 5\bigg) \\ &= 2\bigg(5 + 7 + 9 + 11 + ... + 21 + 23\bigg) + 25 \\ &= 2 \times S_{10} + 25 \\ &= 2 \times 140 + 25 \\ &= 305\ \text{cm} \end{align*})
).
is an AP of 11 terms (weeks 1 to 11, inclusive) which has
,
, and
.
is an AP of 10 terms (weeks 12 to 21, inclusive) which has
,
, and
.
Approach 1(b): Slightly different division of the series
is an AP of 10 terms (weeks 1 to 10, inclusive) which has
,
, and
.
is an AP of 11 terms (weeks 11 to 21, inclusive) which has
,
, and
.
Approach 2: Less obvious but quicker...
. We now have only one set of brackets and a single AP, plus an extra term that needs to be added:
is an AP of 10 terms (weeks 1 to 10, forwards, which is the same as weeks 12 to 21, backwards - inclusive in each case) which has
,
, and
.
