-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
polynomial q (1 Viewer)
- Thread starter yashbb
- Start date
ExtremelyBoredUser
Bored Uni Student
Find the roots of the equation. From the graph you can deduce the correct intercept as one root is approximately 3 and the other is negative so the root that isn't either of them has the correct x value.
see everything, u know it allFind the roots of the equation. From the graph you can deduce the correct intercept as one root is approximately 3 and the other is negative so the root that isn't either of them has the correct x value.
i cant find the -ve rootFind the roots of the equation. From the graph you can deduce the correct intercept as one root is approximately 3 and the other is negative so the root that isn't either of them has the correct x value.
also if you wouldnt mind me asking, how the hell did you get so good.Find the roots of the equation. From the graph you can deduce the correct intercept as one root is approximately 3 and the other is negative so the root that isn't either of them has the correct x value.
ExtremelyBoredUser
Bored Uni Student
The roots aren't integer values so it would be unfeasible to use the remainder theorem for this question. There's a method that I don't think is taught in the new syllabus called Newton's Method. This is pretty much catered for such questions where the roots are decimal based. https://en.wikipedia.org/wiki/Newton's_methodi cant find the -ve root
Alternatively you could use the root equations; sums of roots, mulitiplication of roots (a+b+y) or (aby) and sums of double roots (ab+by+ya) and manipulate them to find each value or get an estimate but that would be more trickier however if you're decent at it, I don't see why not?
I'm going to head off to sleep so perhaps someone else can provide a better method but these are the first things that came to my head to solve this q.
no no they worked so thank you so much! gnightThe roots aren't integer values so it would be unfeasible to use the remainder theorem for this question. There's a method that I don't think is taught in the new syllabus called Newton's Method. This is pretty much catered for such questions where the roots are decimal based. https://en.wikipedia.org/wiki/Newton's_method
Alternatively you could use the root equations; sums of roots, mulitiplication of roots (a+b+y) or (aby) and sums of double roots (ab+by+ya) and manipulate them to find each value or get an estimate but that would be more trickier however if you're decent at it, I don't see why not?
I'm going to head off to sleep so perhaps someone else can provide a better method but these are the first things that came to my head to solve this q.
The biggest piece of advice that I have for a question like this, where an approximation is sought, is not to attempt standard methods like the remainder theorem or root theory unless you are sure that they will yield results. They are likely to be unproductive and a waste of time.
Newton's Method would definitely be a useful tool here, but as has been noted, it's not in the syllabus any longer. So, the simplest method to finding , since you only need one decimal place, is halving the interval. You know the function is continuous, so it can only change sign by passing through a root. From the graph,
, since you only need one decimal place, is halving the interval. You know the function is continuous, so it can only change sign by passing through a root. From the graph,  looks to me to be somewhere near 0.3. So:
looks to me to be somewhere near 0.3. So:
Try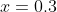 :
:  = f(0.3) = 2(0.3)^3 - 5(0.3)^2 -3(0.3) + 1 = -0.296)
From the graph, we can see that there must be a root between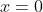 , where
, where  = 1) , and
, and 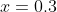 , as
, as  < 0) . In other words, the root we seek at
. In other words, the root we seek at 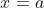 satisfies
satisfies 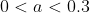 . I could take this as my interval, but since I seek one decimal place, I'd prefer an interval with a width of 0.1 or 0.2. So, I now try
. I could take this as my interval, but since I seek one decimal place, I'd prefer an interval with a width of 0.1 or 0.2. So, I now try 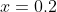 as the root looks to me to be closer to 0.3 than to 0.
as the root looks to me to be closer to 0.3 than to 0.
Trying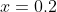 :
:  = 2(0.2)^3 - 5(0.2)^2 -3(0.2) + 1 = 0.216)
We now know that the root we seek at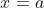 satisfies
satisfies 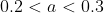 as
as ) changes sign in this interval. To find its value to one decimal place, we need only halve this interval by testing its midpoint.
changes sign in this interval. To find its value to one decimal place, we need only halve this interval by testing its midpoint.
Test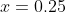 :
:  = 2(0.25)^3 - 5(0.25)^2 -3(0.25) + 1 = -0.03125)
From this, we conclude that the root we seek at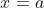 satisfies
satisfies 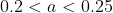 as it changes sign in this domain.
as it changes sign in this domain.
Every value within this interval is the same to one decimal place. Thus,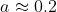 (to one decimal place).
(to one decimal place).
The halving the interval method has several limitations:
Newton's Method would definitely be a useful tool here, but as has been noted, it's not in the syllabus any longer. So, the simplest method to finding
Try
From the graph, we can see that there must be a root between
Trying
We now know that the root we seek at
Test
From this, we conclude that the root we seek at
Every value within this interval is the same to one decimal place. Thus,
The halving the interval method has several limitations:
- you need to start by finding a suitable domain, which is easy in this case given the graph
- the convergence is slow. To find to two decimal places, we'd need to test
, then either
or
, etc. Newton's method allowed for very rapid convergence. There was a 4 unit question from about 1988 (IIRC) that included a proof that 12 applications led to an approximation that was correct to over 200 decimal places.
- there can be multiple roots in an interval. For example, here
changes sign between
and
, and
is continuous on this domain. So, there must be at least one root between
and
, but there could be more than one... as we can see, there are three. Similarly, we can see that
and
are both positive which means that, for a continuous curve like
, there need not be any roots, but it does not prove that there are no roots. There could be two roots (as we can see is the case).
- Having said all of that, Newton's Method also has limitations.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
I reckon this is where we start the show. Differentiate
Personally, I just don't like guessing, so from what I said a is 0.3 but it is wrong I reckon what actually will happen is that the number will round down giving us 0.2. I feel the logic is wrong.


