First and foremost ask yourself what are the two conditions here. Well, the first one is that Walter and Maude do not sit with each other. Next step the couples have to sit together.
Now that this is in the bag we can now focus on Walter and Maude. Well since Walter and Maude cannot sit together then we can start by drawing up a diagram where either Maude or Walter can sit first and then where either Walter or Maude sits you need to ask yourself a question
Well. the next condition is that the couples have to sit together so therefore Maude or Walter must sit in a seat 3 spaces away or a seat that is 5 seats away. Remember you need the 4 couples to sit together. Thus we now have the number 3 which will be mulitplied later.
Next step with the couples this is where things get interesting they can either be man and woman or vice versa and this is where instead of going with the method given I have my own thought use combinatorics which is where how many of the couples alternate. So there I did

+
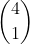
+
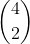
+
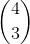
+
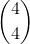
=
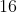
. By itself, this would be 48 ways. Now the hard part is out of the way the last thing we need to do is sort them by the spaces available there are 4 spaces available and then once one couple sits 3 spaces are left over for the remaining couples and so on thus you have 4!.
Multiplying them together you will have
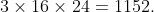
A common technique for these questions go like this.
1. Find the condition where they cannot be something that is important because otherwise something unfavourable will occur.
2. Find the condition where people are together, this has to be resolved next so that things do not get messy.
3. Apply the factorials and finish the question.



