I guess I might have just forgotten - I realise that v = root (gr tan theta) will give us the minimum velocity, however how do we find out the maximum velocity that an object in that radius can travel at? Correct me if I am wrong...
I presume you know the derivation but I'll throw it in for anyone reading the thread new to Mod 5.
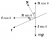
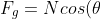 )
(as the forces balance, - if they didn't then how is the car not thrusted downwards or upwards?)
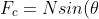 )
(The horizontal component of the normal force provides the centripetal force)
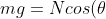 )
therefore
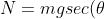 )
(1)
Unpacking the centripetal force equation
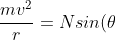 )
substituting (1)
 \times sin(\theta) )
 )
 )
There is no minimum or maximum velocity for a given radius. The object orbits at such radius due to the velocity, and orbits at such velocity for a given radius. g and tan are constant variables most of the times (but tan(theta) can change if the angle of the banked track is reduced or increased) so most of the times your considering the relationship between v and r.
Greater radius will lead to a greater velocity to necessitate the radius of the circular motion as
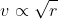
, if there is a change in velocity, there will be a change in radius as stated above since other variables are constant. There can be a maximum and minimum velocity for a given range of radius e.g Whats the minimum/maximum velocity a car can move around a banked track given the distance of the track is X to Y (poor phrasing but I remember Qs like that and I assume you're referring to them) etc.

