Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
inequalities (1 Viewer)
- Thread starter =)(=
- Start date
So you have not written coherently.Find the minimum value of x^2+y^2 given that xy(x^2-y^2)=x^2+y^2 x not = 0
I am not 100% sure however I think Karush-Kuhn-Tucker condition is what you are after given you have additional constraint x != 0.
Not sure how to solve it otherwise.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Is that your questionFind the minimum value of x^2+y^2 given that xy(x^2-y^2)=x^2+y^2 x not = 0
Find the minimum value of
YesIs that your question
Find the minimum value ofgiven that
,
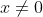
Where did you get the question from?
I have a slight feeling that this could have something to do with complex numbers, cause if you let 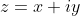
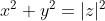 ,
, =x^2-y^2) and
and =xy)
so the equation can be\Re(z^2)) or
or )
I'm not sure where to go on from there, but maybe it could help you.
EDIT
maybe you can say that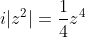 where
where =0)
That is
^2-4x^2y^2=0\\\\x^4-6x^2y^2+y^4=0\\\\\left(\frac{y}{x}\right)^4-6\left(\frac{y}{x}\right)^2+1=0)
Then
^2=\frac{6\pm\sqrt{32}}{2})
so the equation can be
I'm not sure where to go on from there, but maybe it could help you.
EDIT
maybe you can say that
That is
Then
Last edited:
Sorry how did you get this part:I have a slight feeling that this could have something to do with complex numbers, cause if you let
,
and
so the equation can beor
I'm not sure where to go on from there, but maybe it could help you.
EDIT
maybe you can say thatwhere
That is
Then
^2=\frac{6\pm\sqrt{32}}{2})
It was an assumption that ifSorry how did you get this part:
where
=0)
I just made the number
Looking at it now, this is probably wrong. Cause there is no definite reason why
- Joined
- Feb 16, 2005
- Messages
- 8,628
- Gender
- Male
- HSC
- 2006
A bit beyond syllabus but consider a parametric polar form where both r and theta are variables:
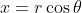
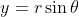
This reduces the condition to
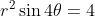
Your objective is to find the minimum value of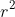 .
.
Since the RHS is fixed, we minimise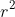 by maximising
by maximising 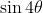 .
.
Hence the minimum value of of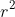 is 4.
is 4.
This reduces the condition to
Your objective is to find the minimum value of
Since the RHS is fixed, we minimise
Hence the minimum value of of
