Driftonian
New Member
- Joined
- Jan 9, 2024
- Messages
- 2
- Gender
- Undisclosed
- HSC
- N/A
le hospital or sub in small values of x (neither of which are in syllabus i think)Any help would be appreciated. Many thanks!
No u fucking retard ass bitchle hospital or sub in small values of x (neither of which are in syllabus i think)
yeah I think this mans approach is pre good. you see the limit then turns to -2limsinx/x*limsinx and taking limx->0sinx=0 thererfore the rhs=0.No u fucking retard ass bitch
u take - out from numerator, then u use double angle formula, take the 2 out and bobs your fucking uncle you dissappointment bitch
Why are you able to split the multiplication of the limits?yeah I think this mans approach is pre good. you see the limit then turns to -2limsinx/x*limsinx and taking limx->0sinx=0 thererfore the rhs=0.
its a property of limits hun lim(f(x)*g(x))=limf(x)*limg(x)Why are you able to split the multiplication of the limits?
Why are you able to split the multiplication of the limits?
^its a property of limits hun lim(f(x)*g(x))=limf(x)*limg(x)
It's not in syllabus don't listen to Bored Of Studying.Why are you able to split the multiplication of the limits?
nah i think it is. its just noting limsinx/x=1 and limsinx=0. I think its basically what u said, but I think you'd lose marks if you don't indicate limfxgx=limfxlimgxIt's not in syllabus don't listen to Bored Of Studying.
yeah prove that tho cuz i don't think it's explicitly stated in syllabusnah i think it is. its just noting limsinx/x=1 and limsinx=0. I think its basically what u said, but I think you'd lose marks if you don't indicate limfxgx=limfxlimgx
Yeah I mean I think it just uses intuition. Like its not explicitly on there, but applying laws of limits, you can see as x->0; sinx->0 and thats ur ans. Kinda is indirectly related/yeah prove that tho cuz i don't think it's explicitly stated in syllabus
While other post have given answer I thought would add more detail. There things called indeterminant forms. Basically if you cannot evaluate a limit using substitution then you have indeterminant form. (E.g., 0/0, 0^0, infinity/infinity, 1^infinity, infinity - infinity, 0*infinity)Why are you able to split the multiplication of the limits?
In Ext 1 Maths, you can assume:Beautifully done!
For anyone confused over why
View attachment 42052
Please find the proof (using Squeeze Theorem) attached!
Yeh I know, but it’s cool to know WHY. Then you can really believe it from there.In Ext 1 Maths, you can assume:
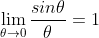
Really easy way is to split the fraction (limit of product is product of limits):Any help would be appreciated. Many thanks!
but lim x-> 0 of 1/x is infinity thoReally easy way is to split the fraction (limit of product is product of limits):
lim x->0 (cosx-1/x) = lim x->0 (1/x) * lim x->0 (cosx-1) =0 * 0 = 0
not to mention it doesnt exist since 1/x goes to -inf from 0- and inf from 0+but lim x-> 0 of 1/x is infinity tho
in general this is not trueinf times zero = zero

