The problem is finding the number of different solutions of the equation
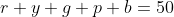
where

is the number of red balls, etc, subject to the constraints that:
Equations like this are called Diophantine equations and the number of solutions can be counted by the "stars and bars" method - neither of which is formally in any HSC course. Without the constraints, the number of combinations / solutions would simply be:
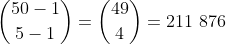
Taking into account the constraint that there must be at least 4 of each colour, and noting that the stars-and-bars approach is designed for at least one of each, we can transform using
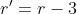
(and similar), so that
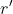
is the number of red balls more than 3, so that the minimum value of
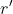
is 1, consistent with how stars-and-bars counting works. This yields:
 + (y' + 3) + (g' + 3) + (p' + 3) + (b' + 3) &= 50 \\ r' + y' + g' + p' + b' &= 50 - 5 \times 3 = 35 \end{align*})
The number of solutions here is then
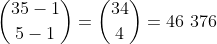
However, this does not account for the constraint that
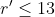
, etc. We now need to count the cases where one or more colours would have too many balls, and subtract those.
Can anyone complete the solution from here?

