-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Ekman's Compilation of MX2 Questions (1 Viewer)
- Thread starter Ekman
- Start date
WeiWeiMan
Well-Known Member
just sub it in lolDyk how to do it
z^13 = w
w^11 = z
z = w^11
= z^(13*11) = z^143
hence z^142 = 1
z is some 142nd root of unity
hence z = cos(2πm/142) + isin(2πm/142) for integer m
Im(z) = sin(2πm/142) = sin(πm/71) = sin(πm/n) where n = 71
Average Boreduser
Rising Renewal
but yea idfk lmfao. imo just do trial papers or smn instead of some dude's decade old compilations that came from an older syllabusYeah i tried thatcis form and shit
kkk579
hello
whats a root of unity?just sub it in lol
z^13 = w
w^11 = z
z = w^11
= z^(13*11) = z^143
hence z^142 = 1
z is some 142nd root of unity
hence z = cos(2πm/142) + isin(2πm/142) for integer m
Im(z) = sin(2πm/142) = sin(πm/71) = sin(πm/n) where n = 71
SMARTYPANTS_SINGH
NESA WHY?
- Joined
- May 22, 2022
- Messages
- 286
- Gender
- Male
- HSC
- 2024
Damn looks like NGO needs to do thatwhats a root of unity?
WeiWeiMan
Well-Known Member
bro whatwhats a root of unity?
an nth root of unity is a complex number of the form z^n=1
these can be written in the form z=cis(2kπ/n) for some integer k
some neat things about roots of unity
sum of roots of unity = 0 {via sum of roots =-b/a}
nth roots of unity can be expressed as 1, w, w^2,..., w^(n-1) where w is some nth root of unity not equal to 1
edit: also, they form regular polygons when graphed in complex plane (argand diagram), (also a cyclic polygon)
SMARTYPANTS_SINGH
NESA WHY?
- Joined
- May 22, 2022
- Messages
- 286
- Gender
- Male
- HSC
- 2024
I think u should learn it towards the end of complex
kkk579
hello
Damn looks like NGO needs to do that
kkk579
hello
Yeah nah ngo hasnt taught us that strangely wtfbro what
an nth root of unity is a complex number of the form z^n=1
these can be written in the form z=cis(2kπ/n) for some integer k
some neat things about roots of unity
sum of roots of unity = 0 {via sum of roots =-b/a}
nth roots of unity can be expressed as 1, w, w^2,..., w^(n-1) where w is some nth root of unity not equal to 1
kkk579
hello
Bruh ngo needa shape their shit cos wtf. Theres one prac q in the classwork book which mentions z^n=1 but nothing abt the line after which u wrote (expressed as z=cis2kpi/n), but the q isnt even similar to this one its different and doesnt use this root of unity = n concept or whateverYeah nah ngo hasnt taught us that strangely wtf
WeiWeiMan
Well-Known Member
maybe it wasn't useful for itBruh ngo needa shape their shit cos wtf. Theres one prac q in the classwork book which mentions z^n=1 but nothing abt the line after which u wrote (expressed as z=cis2kpi/n), but the q isnt even similar to this one its different and doesnt use this root of unity = n concept or whatever
you don't always need z=cis(2kπ/n) for roots of unity questions
if the question mentioned roots of unity, it contains roots of unity bruv
I used roots of unity for Q10 in the compilation however there may exist different approaches that do not use roots of unity
kkk579
hello
Yeah but it was only that one q it wasnt taught explicitly. It was also mentioned in the q to just use z^n=1 so i didnt even actually know that it was roots of unity when i did itmaybe it wasn't useful for it
you don't always need z=cis(2kπ/n) for roots of unity questions
if the question mentioned roots of unity, it contains roots of unity bruv
I used roots of unity for Q10 in the compilation however there may exist different approaches that do not use roots of unity
kkk579
hello
dam. Looks like dr du might do u better it seems.
Domain6938
New Member
- Joined
- Jan 2, 2024
- Messages
- 1
- Gender
- Male
- HSC
- 2024
ag1 crazy rizz brodyI think u should learn it towards the end of complex
sly_lyepat
Active Member
- Joined
- Aug 3, 2024
- Messages
- 107
- Gender
- Male
- HSC
- 2026
does someone have something like this but ext 1 for prelim and year 12
Idk_man122223
New Member
- Joined
- Apr 16, 2025
- Messages
- 5
- Gender
- Undisclosed
- HSC
- 2026
I tried to make some worked solutions to these, seeing as there aren't any already. I didn't include graphs (self explanatory), conics (old syllabus), or mechanics (I haven't learnt it yet). I couldn't do q18 integration, q10 part iii harder 3u, q18 and q20 combinatorics. If you find any issues/have any simpler ways to do any of these please tell me.
(also sorry for the awful formatting, I started with handwriting but it wasn't legible).
(also sorry for the awful formatting, I started with handwriting but it wasn't legible).
Attachments
-
328 KB Views: 15
combinatorics 20 is

how do i know? it is where
where 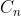 is the (n+1)-th Catalan number: https://en.wikipedia.org/wiki/Catalan_number
is the (n+1)-th Catalan number: https://en.wikipedia.org/wiki/Catalan_number
how do i know? it is
Last edited:
Idk_man122223
New Member
- Joined
- Apr 16, 2025
- Messages
- 5
- Gender
- Undisclosed
- HSC
- 2026
Thank you, this is the most straightforward answer but I wonder if there is also a reasonable way to do it using concepts more familiar to HSC syllabus.
