-
Looking for HSC notes and resources? Check out our Notes & Resources page
2020 Normanhurst Ext 1 Trial Paper Help (1 Viewer)
- Thread starter csi
- Start date
B1andB2
oui oui baguette
Let the roots be alpha, - alpha, beta
sum of roots
alpha + (- alpha) + beta = -1
So beta = -1
product of roots
-alpha^2 x beta = 10
Alpha ^2 = 10 (1)
sum two at a time
- alpha^2 = c (2)
sub 1 into 2
c = -10
for the other one I think the answer is 14
i would do 9C3/3! (Not completely certain)
sum of roots
alpha + (- alpha) + beta = -1
So beta = -1
product of roots
-alpha^2 x beta = 10
Alpha ^2 = 10 (1)
sum two at a time
- alpha^2 = c (2)
sub 1 into 2
c = -10
for the other one I think the answer is 14
i would do 9C3/3! (Not completely certain)
Last edited:
Thank youLet the roots be alpha, - alpha, beta
sum of roots
alpha + (- alpha) + beta = -1
So beta = -1
product of roots
-alpha^2 x beta = 10
Alpha ^2 = 10 (1)
sum two at a time
- alpha^2 = c (2)
sub 1 into 2
c = -10
for the other one I’m pretty sure the answer is 14
i would do 9C3/3!
Let the roots be alpha, - alpha, beta
sum of roots
alpha + (- alpha) + beta = -1
So beta = -1
product of roots
-alpha^2 x beta = 10
Alpha ^2 = 10 (1)
sum two at a time
- alpha^2 = c (2)
sub 1 into 2
c = -10
for the other one I think the answer is 14
i would do 9C3/3! (Not completely certain)
9C3/3! seems kind of sketchy.Thank you
may be better to split it into |---|.
two diagonal combinations of points.
two vertical combinations of points.
5C3 for the horizontal line.
add it up.
Another cool way of doing the poly q: subHi,
Can I please have a hand on these two questions:
Consider the polynomial P(x) = x^3+x^2+cx-10. It is known that two of its zeros are equal in magnitude but opposite in sign. What is the value of c?
(a) root 10
(b) 10
(c) -10
(d) - root 10
View attachment 29844
Thanks!!
At this point you could just use your calculator (since its M.C) but working it out:
OR even better looking at B1B2's response, she found a root
Last edited:
username_2
Active Member
- Joined
- Aug 1, 2020
- Messages
- 116
- Gender
- Male
- HSC
- 2020
hmm for q10.. i dunno if it is 14 just because of the fact that I have tried like 10 different combinations of these 9 dots and a max of 8 combinations is all I found. Might be wrong but I'm just trying to help (I have no real proof - might be pigeonhole principle who knows)Let the roots be alpha, - alpha, beta
sum of roots
alpha + (- alpha) + beta = -1
So beta = -1
product of roots
-alpha^2 x beta = 10
Alpha ^2 = 10 (1)
sum two at a time
- alpha^2 = c (2)
sub 1 into 2
c = -10
for the other one I think the answer is 14
i would do 9C3/3! (Not completely certain)
Do what Idkddi did. 2 combinations diagonally, 2 combinations vertically. Then horizontally 5 dots need to choose 3hmm for q10.. i dunno if it is 14 just because of the fact that I have tried like 10 different combinations of these 9 dots and a max of 8 combinations is all I found. Might be wrong but I'm just trying to help (I have no real proof - might be pigeonhole principle who knows)
ThanksAnother cool way of doing the poly q: subinto the original equation to get:
and
Add these two to get:
i.e.
WLOG. Making c the subject:
At this point you could just use your calculator (since its M.C) but working it out:
OR even better looking at B1B2's response, she found a rootfrom here we can simply sub this into the equation to find c,
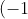^3+(-1)^2-c-10=0 \implies c=-10)

