Dude I’m not joking. Will you write a book?My specialty is challenging the most able students
Addendum: I'm not trying to make anyone feel dumb, though. These are challenging questions. I hope that those students who can't do them will learn something about techniques / approaches and the proof topic by looking at them and their answers.
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2nd order recursion (1 Viewer)
- Thread starter tito981
- Start date
Could you do write up some challenging Q's for Ext1?My specialty is challenging the most able students
Addendum: I'm not trying to make anyone feel dumb, though. These are challenging questions. I hope that those students who can't do them will learn something about techniques / approaches and the proof topic by looking at them and their answers.
Yes, it was the other way around in both cases. Apologies for the typo which happened due to a momentary brain-o! Thanks for pointing it out. I have edited the post to make a correction, noting you as the person who picked it up.(b) Aren't terms in S_E decreasing and S_O increasing (other way around), or am I misundestanding?
...
(d) Again I think it's the other way around?
It's something that I am considering. It's a huge task though, and would need to be done in a way that it was a useful addition to the selection of books already available.Dude I’m not joking. Will you write a book?
Thanks for the encouragement and interest.
I can. If you start a thread in the MX1 forum asking for challenging questions on a particular topic, I'll see what I can put up.Could you do write up some challenging Q's for Ext1?
For part d:Question 10
Consider the function
(a) Discuss the behaviour ofas
for a constant
.
(b) Defineas the set containing the ratios of the (
)-th to the
-th Fibonacci number for integers
and construct two sequences,
, and
. That is
Are these sequences finite? Are they bounded? Discuss.
(c) Hence, using part (a) or otherwise, and assuming that the terms inare strictly
increasingdecreasing and those inare strictly
decreasingincreasing, prove that both sequences approach the same limit and find it.
(d) Challenge: Prove that the terms inare strictly
increasingdecreasing and those inare strictly
decreasingincreasing.
Edit note: Following Qeru's post below, I have corrected my mistake in mixing up increasing (which is what the terms in the sequenceare doing) and decreasing (which is what the terms in the sequence
are doing). I have also modified the start of part (c) so that it is a "hence or otherwise" question.
R.T.P
I will use Binet's formula again (I feel like I'm abusing it at this point lol):
but:
So in total
Same idea for S_E
Fixed thanks to CMtutor
Last edited:
The mistake is in the quoted bolded part in red, as...
So in totalsince psi and phi are both positive
...
Im getting the opposite of what is required, I checked my alegbra and signs carefully and there seems to be no error, what did I do wrong?
I'd left question 2 and thought I should come back to it...
Question 2
(a) List the values of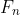 for
for 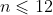 and note the pattern of the even terms in the sequence. State a theorem related to generalise this pattern and prove it without using induction.
and note the pattern of the even terms in the sequence. State a theorem related to generalise this pattern and prove it without using induction.
(b) Use induction to show that all terms of the form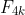 are divisible by 3.
are divisible by 3.
(c) Prove that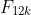 is a multiple of 12. You may use the fact that
is a multiple of 12. You may use the fact that 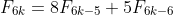 .
.
Solution to 2(a)
What I intended was that
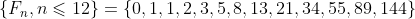
And the even terms, that is, the terms that are even, are ,
,  ,
, 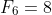 ,
, 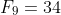 , and
, and 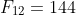 . The pattern I sought was that terms of the form
. The pattern I sought was that terms of the form 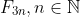 , are even. This can easily proven by induction, but also by noting that the terms follow a pattern of even - odd - odd - even - odd - odd - even - odd - odd - etc. Using the recursive formula from
, are even. This can easily proven by induction, but also by noting that the terms follow a pattern of even - odd - odd - even - odd - odd - even - odd - odd - etc. Using the recursive formula from 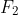 , and noting that
, and noting that
Solution to 2(b)
Theorem: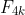 is divisible by 3 for all
is divisible by 3 for all 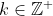
Proof: By induction on
A Put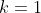 :
:
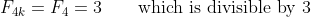
B Put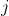 be a value of
be a value of  for which the result is true,
for which the result is true,
That is, let})
We must now prove the result for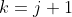 .
.
That is, we must prove that} = 3N \qquad \text{for some integer $N$})
} \\ &= F_{4j+4} \\ &= F_{4j+3} + F_{4j+2} \qquad \text{using the recursive definition of the Fibonacci Sequence, $F_n = F_{n-1} + F_{n-2}$, with $n=4j+4$} \\ &= \left(F_{4j+2} + F_{4j+1}\right) + F_{4j+2} \qquad \text{using the recursive definition of the Fibonacci Sequence with $n=4j+3$} \\ &= 2F_{4j+2} + F_{4j+1} \\ &= 2\left(F_{4j+1} + F_{4j}\right) + F_{4j+1} \qquad \text{using the recursive definition of the Fibonacci Sequence with $n=4j+2$} \\ &= 3F_{4j+1} + 2F_{4j} \\ &= 3F_{4j+1} + 2 \times 3M \qquad \text{using the induction hypothesis (**)} \\ &= 3N \qquad \text{where $N = F_{4j+1} + 2M$ is an integer} \\ &= \text{ RHS} \end{align*})
So, if the result is true for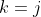 , then it follows that the result is also true for
, then it follows that the result is also true for 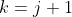 .
.
C It follows from A and B by the process of mathematical induction that the result is true for all positive integers .
.
Solution to 2(c)
The theorem that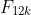 must be a multiple of 12 (for all positive integers
must be a multiple of 12 (for all positive integers  ) can be done in exactly the same way as (b), but deriving the necessary result in part B of the proof is long. It can be shortened by using the given result, but there is a better option still.
) can be done in exactly the same way as (b), but deriving the necessary result in part B of the proof is long. It can be shortened by using the given result, but there is a better option still.
We have seen that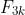 is divisible by 2 and that
is divisible by 2 and that 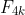 is divisible by 3, and
is divisible by 3, and 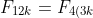}) so
so 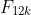 must be divisible by 3 (and also by 2). Any integer
must be divisible by 3 (and also by 2). Any integer 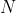 that is divisible by both
that is divisible by both  and
and 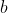 must be divisible by
must be divisible by 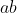 so long as
so long as  and
and 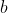 are coprime. Our given result points to finding a property of
are coprime. Our given result points to finding a property of 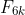 , which is that
, which is that 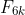 is divisible by 4.
is divisible by 4.
Theorem: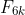 is divisible by 4 for all
is divisible by 4 for all 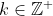
Proof: By induction on
A Put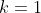 :
:
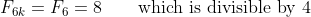
B Put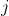 be a value of
be a value of  for which the result is true,
for which the result is true,
That is, let})
We must now prove the result for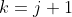 .
.
That is, we must prove that} = 4N \qquad \text{for some integer $N$})
} \\ &= F_{6j+6} \\ &= 8F_{6j+6-5} + 5F_{6j+6-6} \qquad \text{using the given result $F_{6k} = 8F_{6k-5} + 5F_{6k-6}$ with $k=j+1$} \\ &= 8F_{6j+1} + 5F_{6j} \\ &= 8F_{6j+1} + 5 \times 4M \qquad \text{using the induction hypothesis (**)} \\ &= 4N \qquad \text{where $N = 2F_{6j+1} + 5M$ is an integer} \\ &= \text{ RHS} \end{align*})
So, if the result is true for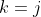 , then it follows that the result is also true for
, then it follows that the result is also true for 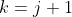 .
.
C It follows from A and B by the process of mathematical induction that the result is true for all positive integers .
.
We know that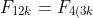}) is divisible by 3 from part (b).
is divisible by 3 from part (b).
We now know that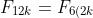}) is divisible by 4 from the above induction proof.
is divisible by 4 from the above induction proof.
3 and 4 are coprime, they share no common factors except for 1, and so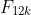 is divisible by
is divisible by 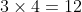 , as required.
, as required.
Question 2
(a) List the values of
(b) Use induction to show that all terms of the form
(c) Prove that
Solution to 2(a)
What I intended was that
And the even terms, that is, the terms that are even, are
Solution to 2(b)
Theorem:
Proof: By induction on
A Put
B Put
That is, let
We must now prove the result for
That is, we must prove that
So, if the result is true for
C It follows from A and B by the process of mathematical induction that the result is true for all positive integers
Solution to 2(c)
The theorem that
We have seen that
Theorem:
Proof: By induction on
A Put
B Put
That is, let
We must now prove the result for
That is, we must prove that
So, if the result is true for
C It follows from A and B by the process of mathematical induction that the result is true for all positive integers
We know that
We now know that
3 and 4 are coprime, they share no common factors except for 1, and so
