another complex question (1 Viewer)

[juantheron]

 

[muhahahahaha]

Yeah that is hard I don't know

 

[Carrotsticks]

I have to admit this was one of the more difficult locus questions I have come across.

The solution (algebraically) is quite long, but I'll outline the general steps.

If you are attempting these sorts of questions, I am sure that your ability is great enough to be able to get to the answer after being given a bit of a push in the right direction:

1. Recognise that we can use the triangle inequality in the LHS. You will get something like | XXXXX | <= 3sqrt(5)

2. Remember that if |x| <= a, then -a <= x <= a. We make two inequalities this way. So you should get something like -3sqrt(5) <= | XXXXX | <= 3sqrt(5)

3. For the | XXXXX | part, simplify the inside so then you get one big fraction.

4. Solve the two inequalities for z.

I tried doing it geometrically, but adding the equations of two (well... one and a half haha) circles with one of them being magnified by a scale of 20 got a bit too difficult.

 

[deterministic]

Although to do it properly is difficult, using some tricks make it easy. These tricks shouldn't really be used for normal questions. This is really a more educated trial and error keeping in mind the design of the question.

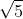
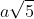
The idea is to note that since we are adding 2 real numbers on left hand side, the easiest way to get as a total is to assume it appears on both terms. In other words |z| should be for some real positive a.

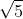
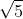
We note since 2+i part of the denominator has a modulus of , we see that it is ideal if z is a multiple of 2+i as then we will get the term we need.

So let z=a(2+i) for some real number a. Then we can sub it in to get:


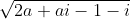
As for the rest, you can either solve it properly or note that again we dont want another irrational term in so we choose a=1 to guarantee that the real parts disappear. Either way you get the answer is z=2+i. But this method is pretty bs to be honest and you don't learn much from doing this question.