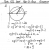-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
arg diagrams (1 Viewer)
- Thread starter kkk579
- Start date
kkk579
hello
kkk579
hello
fluffchuck
Active Member
The idea behind your region shading is correct! Just be careful with how you position the lines for the arg locus & the circle for the modulus locus - hint: the arg locus stems from the point (1,1), does this point (1,1) lie inside the circle, or does it lie on the circle?for this graph it was to shade -pi/2 <= arg <= - pi then the bottom greater part would be shaded rightView attachment 45867View attachment 45868
fluffchuck
Active Member
the big angle on the diagram is pi/3,
the small angle on the diagram is pi
I take this back, you are correct - the angle is indeed a negative angle, and it should be -[(big angle on diagram) - (small angle on diagram)] = (small angle on diagram) - (big angle on diagram)
Last edited:
fluffchuck
Active Member
The reason why the Cambridge solution & the Fort St solution is a bit different is because:For the cambridge q, it says that the range of arg(Z) is the same cos its just z being shifted but howcome the same logic doesnt apply to the other q i attached? I understand how the fort st q arrives to the answer but im js confused because the 2 solutions seem a bit contradictoryView attachment 45871View attachment 45872View attachment 45873View attachment 45874
- In the Cambridge question, part (b) shifts both the argument and the circle by 2 units to the left, i.e. |z-2|=1 becomes |z|=1, and arg(z) becomes arg(z+2). As a result, the diagram would look exactly like (a), but everything is just moved 2 units to the left.
- In the Fort st question, the circle remains stationary, and only the argument shifts, i.e. the question contains arg(z), arg(z-1), and arg(z-2). As such, the circle remains still, whereas the arguments are constantly moving relative to the circle.
Hope this helps!
kkk579
hello
thank you this helps alot!The reason why the Cambridge solution & the Fort St solution is a bit different is because:
- In the Cambridge question, part (b) shifts both the argument and the circle by 2 units to the left, i.e. |z-2|=1 becomes |z|=1, and arg(z) becomes arg(z+2). As a result, the diagram would look exactly like (a), but everything is just moved 2 units to the left.
- In the Fort st question, the circle remains stationary, and only the argument shifts, i.e. the question contains arg(z), arg(z-1), and arg(z-2). As such, the circle remains still, whereas the arguments are constantly moving relative to the circle.
Hope this helps!
kkk579
hello
wait but why is it the outside part i thought it would be the larger bottom bitThe idea behind your region shading is correct! Just be careful with how you position the lines for the arg locus & the circle for the modulus locus - hint: the arg locus stems from the point (1,1), does this point (1,1) lie inside the circle, or does it lie on the circle?
fluffchuck
Active Member
Sorry I'm not sure if I'm following - what do you mean by this?wait but why is it the outside part i thought it would be the larger bottom bit
kkk579
hello
Like as in why do u shade the part i attached in the photo and not the region below the 2 perpendicular raysSorry I'm not sure if I'm following - what do you mean by this?
fluffchuck
Active Member
It is because the question is looking for -pi/2 <= arg(z - 1 - i) <= pi, the bit that isn't shaded in your diagram represents -pi <= arg(z - 1 - i) <= -pi/2Like as in why do u shade the part i attached in the photo and not the region below the 2 perpendicular rays