How about the solution of:
The number 2008! (factorial 2008) means the product of all the integers 1,2,3,4,...,2007,2008. With how many zeroes does 2008! end?
Tomorrow's the competition, and I need to know the solution of this wuestions, please? Thanks

The amount of zeros a number ends in is the amount of 10s that are in the prime factorization. Now 10 = 2 x 5. And so when we prime factorize 2008! we need to count the amount of 2s and the amount of 5s.
Now there is clearly going to be more 2s than 5s, so to determine how many factors of 10 there are in the prime factorization of 2008! we must only find how many 5s are in the prime factorization.
Now clearly finding the prime factorization of 2008! would be a torturous task, so we will "look" at each term of 2008! ie 1, 2, 3, 4, 5, 6, . . . ,2007, 2008.
So how many multiples 5s are there between 1 and 2008, well
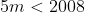
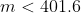
As m is an integer then there are 401.
Now some terms in the prime factorization will have 25 as a factor, and hence that terms will have 2 factors of 5. So we must count how many terms are multiples of 25. Now we already have counted 1 of those factors of 5 (out of those numbers that are multiples of 5^2), and so when we determine how many factors are multiples of 5^2, they will add 1 extra multiple of 5 into our count.
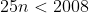

As n is an integer then there are 80.
But some of the factors of 2008! will be multiples of 5^3 = 125, so when we count these by the same logic as before they will contribute an extra 1 multiple of 5 into our count, so
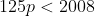
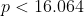
As p is an integer then there are 16.
But some of the factors of 2008! will be multiples of 5^4 = 625, and so these will add an extra 1 multiple of 5 into our count. So,
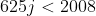
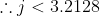
As j is an integer there are 3 of these.
As 5^5 is greater than 2008, then there are no multiples of 5^5 up to 2008.
So in total the amount of factors of 5 in 2008! are
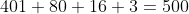
Therefore there are 500 factors of 10 in 2008! and hence 2008! ends in 500 zeros.
Good luck everyone for the competition today =)

