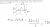dan964
what
Just a friendly reminder, that AMC papers are copyrighted. While we permit posting of individual questions at a time, posting sites that host AMC (Australian Maths Competition), AIMO papers is not allowed.
Please remember this for future.
Please remember this for future.