Now, MrGresh, you go to ask a question. It is very much not being a doofus - first, because it is always good to ask questions, and second, because you are right and have highlighted a point where Jazz has made a small error, and even his answer doesn't entirely address it (Sorry, Jazz):
I don't agree that the "lamp therefore produces specific wavelengths of light that can only be absorbed by strontium ions in the sample." AES is used to identify (qualitatively) what elements are present in a sample, and can then be followed with an AAS analysis to quantify the amount present in an element-specific analysis, but it is subject to interferences. The point of using a lamp with the element to be analysed (strontium, in this case) is that the emissions from the lamp will be caused by transitions between energy levels of strontium, and so will exactly correspond to absorbance wavelengths of strontium. However, this does not mean that those specific wavelengths are unique to strontium. It is possible (though unlikely) to have another substance in the sample that happens to absorb precisely the same wavelength or even produce an emission at exactly that wavelength. In either case, the absorbance data can be effected. The collection of a blank measurement for subtraction is a good technique to avoid such problems, and as Jazz notes, some techniques like UV-Vis typically have a blank sample so that the instrument measures the difference between the samples and not the absolute absorbance of the sample being tested.
Second,
A v.
c data for an AAS will not be linear if the concentration data are wrong. The calibration data will usually be collected from several samples prepared by serial dilution, but if the experimenter's technique is sloppy, the data will be noisy and the line of best fit could easily miss the origin.
Third, AAS stands for
atomic absorption spectroscopy and it depends on the measurement being made on single atoms / ions that are unbound. This is achieved by aspirating (spraying) the sample into a flame where the solvent is vapourised and any species bound to the metal centre in question will be burned away. This is why the element is often complexed either to water or to a suitable organic ligand, so that the bare atom or ion will be quickly produced / released in the environment of the flame, by processes such as:
[Sr(H
2O)
6]
2+(aq) -----in a flame-----> Sr
2+(g) + 6 H
2O(g)
[Sr(EDTA)]
2-(aq) +
a O
2(g) -----in a flame-----> Sr
2+(g) +
x CO
2O(g) +
y H
2O(g) +
z NO(g)
EDTA
4- is a ligand with formula [CH
2N(CO
2)
2]
24- that will burn away and release the strontium ion as an monatomic species.
Unfortunately, some materials that can be present in a sample may bind tightly to the metal centre and cause the measured absorbance to be suppressed. For example, trying to measure the concentration of calcium ions in the presence of phosphate is difficult. Even if Na
4EDTA is added and so there is a competitive equilibrium between [Ca(EDTA)]
2- and whatever calcium / phosphate species are present, the measured concentration of calcium will be an underestimate - and the extent of the underestimate will depend on the relative amounts of each species present, one reason being that it depends whether the sample
Q reaches the value of the
Ksp for Ca
3(PO
4)
2.
Fourthly, looking at Q31 of the BoS paper, there does appear to be one line (the right-most on the Li emission spectra) that is at least very close to the wavelength of a line for Sr... so it would be wise to perform AAS using a Sr line that is not that line, to avoid the possibility of accidental interference from Li.
All of this comes back to the fact that you may get a non-linear
A v.
c graph for the calibration or inaccurate measurements for the unknown sample that are due to a technique problem or to an interference for which account has not been taken. More broadly, it is very poor science to add or subtract from an empirical data set without very good cause and suitable documentation / explanation. Interpolate with care. Extrapolate with great care. And avoid unreasonable / unjustified / unstated assumptions.
On the marking question, I agree with Trebla - there is nothing wrong with interpolating only and not extrapolating unless the circumstances direct you otherwise, either implicitly or explicitly).
Now, looking at the 2020 HSC, Q25, I disagree with Jazz about how that graph should be drawn.
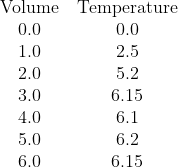
In his answers, Jazz has done what I think many students will do and drawn a diagonal line through
O that bends and becomes a horizontal line. I hope he'll agree (on reflection) that this is not the right thing to do.
We have clearly two parts to the data. One part, with low volumes of citric acid, where the temperature change is increasing as citric acid is the limiting reagent, and a second part, for higher volumes, where citric acid is present in excess and thus the increase in temperature has stablised. Note that water was added to the citric acid solution so that each sample has the same total volume and mass of solution being heated so that the temperature change once the citric acid is present in excess is not being reduced by additional liquid to heat.
We seek the point where there is enough citric acid to consume all of the sodium hydroxide, but no excess.
The correct analysis is:
- Recognise that all the available data needs to be sub-divided into two data sets:
- Data set one (citric acid limiting) contains the volume data for 0.0 mL, 1.0 mL, and 2.0 mL
- Data set two (citric acid in excess) contains the data for 3.0 mL, 4.0 mL, 5.0 mL, and 6.0 mL
- Plot all the points
- Draw the interpolated (diagonal) line of best fit for data set one over the volume range of 0.0 to 2.0 mL (It should be roughly T = 2.567V)
- Draw the interpolated (likely horizontal) line of best fit for data set two over the volume range of 3.0 to 6.0 mL (It should be T = 6.15)
- Extrapolate the diagnoal line of best fit forward until 3.0 mL
- Extrapolate the horizontal line of best fit backwards until 2.0 mL
- The two dotted lines should meet. At the point of intersection, draw a vertical (dashed) line down to the Volume (x) axis. This position is the volume of citric acid that you seek, where the citric acid and sodium hydroxide are present in their stoichiometric ratio and neither is in excess. It is very close to V = 2.4 mL. Stating this value should be the start of your calculations, which should get [NaOH] = 0.96 mol L-1
I would absolutely be penalising an answer with a curve between
V = 2.0 mL and
V = 3.0 mL, firstly as this shows a failure to recognise that there are two data sets, secondly it suggests that the temperature will cease to increase linearly with added citric acid while it remains the limiting reagent, and thirdly because it misses that the experiment has three phases - citric acid limiting, citric acid in excess, and citric acid and sodium hydroxide present in exactly their stoichiometric ratio, which is the only place that the calculation that follows is valid.

